【题目】如图1,△ABC中,沿∠BAC的平分线AB1折叠,剪掉重叠部分;将余下部分沿∠B1A1C的平分线A1B2折叠,剪掉重叠部分;…;将余下部分沿∠BnAnC的平分线AnBn+1折叠,点Bn与点C重合.无论折叠多少次,只要最后一次恰好重合,我们就称∠BAC是△ABC的好角.
小丽展示了确定∠BAC是△ABC的好角的两种情形.情形一:如图2,沿等腰三角形ABC顶角∠BAC的平分线AB1折叠,点B与点C重合;情形二:如图3,沿△ABC的∠BAC的平分线AB1折叠,剪掉重叠部分;将余下部分沿∠B1A1C的平分线A1B2折叠,此时点B1与点C重合.
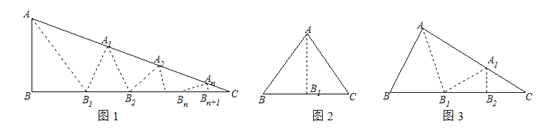
(1)小丽经过三次折叠发现了∠BAC是△ABC的好角,请探究∠B与∠C(不妨设∠B>∠C)之间的等量关系.
(2)根据以上内容猜想:若经过n次折叠∠BAC是△ABC的好角,则∠B与∠C(不妨设∠B>∠C)之间的等量关系为 ;
(3)如果一个三角形的最小角是15°,且满足该三角形的三个角均是此三角形的好角,则此三角形另两个角的度数为 .
参考答案:
【答案】(1)∠B=3∠C;(2)∠B=n∠C;(3)15°,150°.
【解析】试题分析:(1)仔细分析题意根据折叠的性质及“好角”的定义即可作出判断;
(2)因为经过三次折叠∠BAC是△ABC的好角,所以第三次折叠的![]() 由
由![]() 又
又![]()
![]() 由此即可求得结果;
由此即可求得结果;
(3)因为最小角是15°是△ABC的好角,根据好角定义,则可设另两角分别为![]() (其中
(其中![]() 都是正整数),由题意得
都是正整数),由题意得![]() 所以
所以![]() 再根据
再根据![]() 都是正整数可得
都是正整数可得 ![]() 与
与![]() 是
是![]() 的整数因子,从而可以求得结果
的整数因子,从而可以求得结果
试题解析:(1)△ABC中,∠B=2∠C,经过两次折叠,∠BAC是△ABC的好角;
理由如下:小丽展示的情形二中,
∵沿∠BAC的平分线![]() 折叠,
折叠,
∴![]()
又∵将余下部分沿![]() 的平分线
的平分线![]() 折叠,此时点
折叠,此时点![]() 与点C重合,
与点C重合,
∴![]()
∵![]() (外角定理),
(外角定理),
∴∠B=2∠C;
故答案是:是;
(2)∠B=3∠C;
在△ABC中,沿∠BAC的平分线![]() 折叠,剪掉重复部分;将余下部分沿
折叠,剪掉重复部分;将余下部分沿![]() 的平分线
的平分线![]() 折叠,剪掉重复部分,将余下部分沿
折叠,剪掉重复部分,将余下部分沿![]() 的平分线
的平分线![]() 折叠,点
折叠,点![]() 与点C重合,则∠BAC是△ABC的好角.
与点C重合,则∠BAC是△ABC的好角.
证明如下:∵根据折叠的性质知, ![]()
∴根据三角形的外角定理知, ![]()
∵根据四边形的外角定理知, ![]()
根据三角形ABC的内角和定理知, ![]()
∴∠B=3∠C;
由小丽展示的情形一知,当∠B=∠C时,∠BAC是△ABC的好角;
由小丽展示的情形二知,当∠B=2∠C时,∠BAC是△ABC的好角;
由小丽展示的情形三知,当∠B=3∠C时,∠BAC是△ABC的好角;
故若经过n次折叠∠BAC是△ABC的好角,则∠B与∠C(不妨设∠B>∠C)之间的等量关系为∠B=n∠C;
故答案为:∠B=3∠C;∠B=n∠C
(3)由(2)知,∠B=n∠C,∠BAC是△ABC的好角,
因为最小角是![]() 是△ABC的好角,
是△ABC的好角,
根据好角定义,则可设另两角分别为![]() (其中m、n都是正整数).
(其中m、n都是正整数).
由题意,得![]() 所以m(n+1)=11
所以m(n+1)=11
因为m、n都是正整数,所以m与n+1是![]() 的整数因子,
的整数因子,
因此有: ![]()
所以m=1,n=10.
所以![]()
所以该三角形的另外两个角的度数分别为:15°,150°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AO、BO、CO、DO分别是四边形ABCD的四个内角的平分线。
(1)判断∠AOB与∠COD有怎样的数量关系,为什么?
(2)若∠AOD=∠BOC,AB、CD有怎样的位置关系,为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】现有边长分别为a,b的正方形Ⅰ号和Ⅱ号,以及长为a,宽为b的长方形Ⅲ号卡片足够多,我们可以选取适量的卡片拼接成几何图形.(卡片间不重叠、无缝隙)

尝试解决:(1)图1是由1张Ⅰ号卡片、1张Ⅱ号卡片、2张Ⅲ号卡片拼接成的正方形,那么这个几何图形表示的等式是 ;
(2)小聪想用几何图形表示等式(a+b)(2a+b)=2a2+3ab+b2,图2给出了他所拼接的几何图形的一部分,请你补全图形;
(3)小聪选取1张Ⅰ号卡片、3张Ⅱ号卡片、4张Ⅲ号卡片拼接成一个长方形,那么拼接的几何图形表示的等式是 ;

拓展研究:
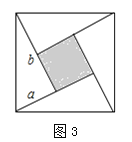
(4)如图3,大正方形的边长为m,小正方形的边长为n,若用m、n表示四个直角三角形的两直角边边长(b>a),观察图案,以下关系式中正确的有 .(填写序号)
①ab=
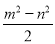 ;②a+b=m;③a2+b2=m2;④a2+b2=
;②a+b=m;③a2+b2=m2;④a2+b2= .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】将纸片△ABC沿DE折叠使点A落在A′处的位置.
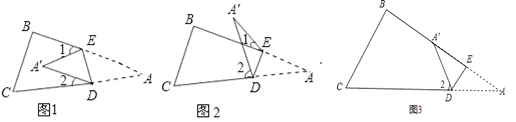
(1)如果A′落在四边形BCDE的内部(如图1),∠A′与∠1+∠2之间存在怎样的数量关系?并说明理由.
(2)如果A′落在四边形BCDE的BE边上,这时图1中的∠1变为0°角,(如图3)则∠A′与∠2之间的关系是 .
(3)如果A′落在四边形BCDE的外部(如图2),这时∠A′与∠1、∠2之间又存在怎样的数量关系?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】全民健身和医疗保健是社会普遍关注的问题.2014年,某社区共投入30万元用于购买健身器材和药品.2015年,该社区购买健身器材的费用比上一年增加50%,购买药品的费用比上一年减少
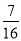 ,但社区在这两方面的总投入仍与2014年相同.
,但社区在这两方面的总投入仍与2014年相同.(1)求2014年社区购买药品的总费用;
(2)据统计,2014年该社区积极健身的家庭达到200户,但其药品费用明显减少,只占当年购买药品总费用的
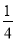 .与2014年相比,如果2015年社区内健身家庭户数增加的百分数与平均每户健身家庭的药品费用降低的百分数相同,那么,2015年该社区用于健身家庭的药品费用就是当年购买健身器材费用的
.与2014年相比,如果2015年社区内健身家庭户数增加的百分数与平均每户健身家庭的药品费用降低的百分数相同,那么,2015年该社区用于健身家庭的药品费用就是当年购买健身器材费用的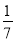 .求2015年该社区健身家庭的户数.
.求2015年该社区健身家庭的户数. -
科目: 来源: 题型:
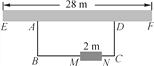
查看答案和解析>>【题目】如图,利用一面墙(墙EF最长可利用28米),围成一个矩形花园ABCD.与墙平行的一边BC上要预留2米宽的入口(如图中MN所示,不用砌墙).现有砌60米长的墙的材料.
(1)当矩形的长BC为多少米时,矩形花园的面积为300平方米;
(2)能否围成480平方米的矩形花园,为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CN是等边△
 的外角
的外角 内部的一条射线,点A关于CN的对称点为D,连接AD,BD,CD,其中AD,BD分别交射线CN于点E,P.
内部的一条射线,点A关于CN的对称点为D,连接AD,BD,CD,其中AD,BD分别交射线CN于点E,P.(1)依题意补全图形;
(2)若
 ,求
,求 的大小(用含
的大小(用含 的式子表示);
的式子表示);(3)用等式表示线段
 ,
,  与
与 之间的数量关系,并证明.
之间的数量关系,并证明.
相关试题

