Question

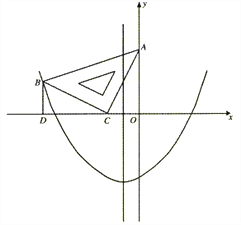
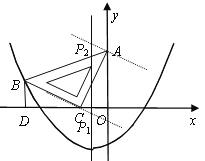
【题目】在平面直角坐标系中，现将一块等腰直角三角板ABC放在第二象限，斜靠在两坐标轴上，点C为 (－1，0) ．如图所示，B点在抛物线y＝x2＋x－2图象上，过点B作BD⊥x轴，垂足为D，且B点横坐标为－3．

（1）求证：△BDC≌△COA；

（2）求BC所在直线的函数关系式；

（3）抛物线的对称轴上是否存在点P，使△ACP是以AC为直角边的直角三角形？若存在，求出所有点P的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）先根据同角的余角相等证得，又为等腰直角三角形，可得．即可证得结论；（2）；（3）

【解析】试题分析：（1）先根据同角的余角相等证得，又为等腰直角三角形，可得．即可证得结论；

（2）由C点坐标可得BD=CO=1，即可得到B点坐标 设所在直线的函数关系式为，根据待定系数法即可求得结果；

（3）先求得抛物线的对称轴为直线．再分以为直角边，点为直角顶点；以为直角边，点为直角顶点，两种情况根据一次函数的性质求解即可.

（1）∵， ，

∴．

∵为等腰直角三角形，

∴．

在和中

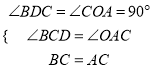
∴（AAS）．

（2）∵C点坐标为，

∴BD=CO=1．

∵B点的横坐标为，

∴B点坐标为．

设所在直线的函数关系式为，

则有，解得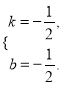

∴BC所在直线的函数关系式为．

（3）存在．

=，

∴对称轴为直线．

若以为直角边，点为直角顶点，对称轴上有一点，使．

∵

∴点为直线与对称轴直线的交点．

由题意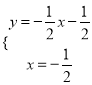得，解得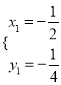

∴．

若以为直角边，点为直角顶点，对称轴上有一点，使，

过点作，交对称轴直线于点．

∵CD=OA，

∴A（0，2）．

易求得直线的解析式为，

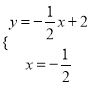由得，∴．

∴满足条件的点有两个，坐标分别为．