【题目】如图,△ABC中,∠BAC=60°,∠ABC=45°,AB=2 ![]() ,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB,AC于E,F,连接EF,则线段EF长度的最小值为 .
,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB,AC于E,F,连接EF,则线段EF长度的最小值为 . 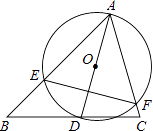
参考答案:
【答案】![]()
【解析】解:由垂线段的性质可知,当AD为△ABC的边BC上的高时,直径AD最短,
如图,连接OE,OF,过O点作OH⊥EF,垂足为H,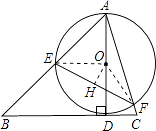
∵在Rt△ADB中,∠ABC=45°,AB=2 ![]() ,
,
∴AD=BD=2,即此时圆的直径为2,
由圆周角定理可知∠EOH= ![]() ∠EOF=∠BAC=60°,
∠EOF=∠BAC=60°,
∴在Rt△EOH中,EH=OEsin∠EOH=1× ![]() =
= ![]() ,
,
由垂径定理可知EF=2EH= ![]() .
.
所以答案是: ![]() .
.
【考点精析】解答此题的关键在于理解垂径定理的相关知识,掌握垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧,以及对圆周角定理的理解,了解顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某校学生的身高情况,随机抽取该校男生、女生进行抽样调查.
已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制如下统计图表:(A组:x<155;B组:155≤x<160;C组:160≤x<165;D组165≤x<170;E组:x≥170)
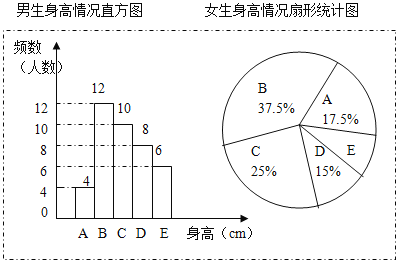
根据图表提供的信息,回答下列问题:
(1)样本中,男生的身高众数在 组,中位数在 组.
(2)样本中,女生的身高在E组的人数有 人.
(3)已知该校共有男生400人,女生380人,请估计身高在160≤x<170之间的学生约有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题。
端午节期间,某食堂根据职工食用习惯,用700元购进甲、乙两种粽子260个,其中甲种粽子比乙种粽子少用100元,已知甲种粽子单价比乙种粽子单价高20%,乙种粽子的单价是多少元?甲、乙两种粽子各购买了多少个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】勾股定理是几何中的一个重要定理.在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的,∠BAC=90°,AB=3,AC=4,点D,E,F,G,H,I都在矩形KLMJ的边上,则矩形KLMJ的面积为( )
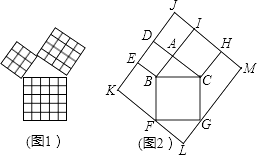
A.90
B.100
C.110
D.121 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=90°,∠A=30°.

(1)用尺规作图作AB边上的中垂线DE,交AC于点D,交AB于点E.(保留作图痕迹,不要求写作法和证明);
(2)连接BD,求证:BD平分∠CBA.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示.根据图中的数据(单位:m),解答下列问题:
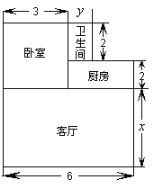
(1)用含
 、
、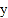 的代数式表示地面总面积;
的代数式表示地面总面积; (2)若
 =5,
=5,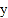 =
= ,铺1m2地砖的平均费用为80元,那么铺地砖的总费用为多少元?
,铺1m2地砖的平均费用为80元,那么铺地砖的总费用为多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】|a|+|b|=|a+b|,则a,b关系是( )
A. a,b的绝对值相等
B. a,b异号
C. a+b的和是非负数
D. a、b同号或a、b其中一个为0
相关试题

