【题目】如图,四边形ABCD内接于⊙O,BD是⊙O的直径,过点A作AE⊥CD,交CD的延长线于点E,DA平分∠BDE.
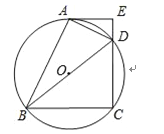
1)求证:AE是⊙O的切线;
(2)已知AE=8cm,CD=12cm,求⊙O的半径.
参考答案:
【答案】(1)AE是⊙O的切线;
(2)⊙O的半径为10cm.
【解析】
试题分析:(1)根据等边对等角得出∠ODA=∠OAD,进而得出∠OAD=∠EDA,证得EC∥OA,从而证得AE⊥OA,即可证得AE是⊙O的切线;
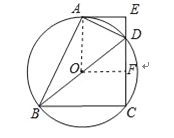
(2)过点O作OF⊥CD,垂足为点F.从而证得四边形AOFE是矩形,得出OF=AE=8cm,根据垂径定理得出DF=![]() CD=6cm,在Rt△ODF中,根据勾股定理即可求得⊙O的半径.
CD=6cm,在Rt△ODF中,根据勾股定理即可求得⊙O的半径.
试题解析:(1)证明:连结OA.
∵OA=OD,
∴∠ODA=∠OAD.
∵DA平分∠BDE,
∴∠ODA=∠EDA.
∴∠OAD=∠EDA,
∴EC∥OA.
∵AE⊥CD,
∴OA⊥AE.
∵点A在⊙O上,
∴AE是⊙O的切线.
(2)解:过点O作OF⊥CD,垂足为点F.
∵∠OAE=∠AED=∠OFD=90°,
∴四边形AOFE是矩形.
∴OF=AE=8cm.
又∵OF⊥CD,
∴DF=![]() CD=6cm.
CD=6cm.
在Rt△ODF中,![]() =10cm,
=10cm,
即⊙O的半径为10cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,AB是⊙O的一条弦,点C是优弧
 上一点.
上一点.(1)若∠ACB=45°,点P是⊙O上一点(不与A、B重合),则∠APB= ;
(2)如图②,若点P是弦AB与
 所围成的弓形区域(不含弦AB与
所围成的弓形区域(不含弦AB与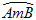 )内一点.求证:∠APB>∠ACB;
)内一点.求证:∠APB>∠ACB;(3)请在图③中直接用阴影部分表示出在弦AB与
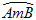 所围成的弓形区域内满足∠ACB<∠APB<2∠ACB的点P所在的范围.
所围成的弓形区域内满足∠ACB<∠APB<2∠ACB的点P所在的范围.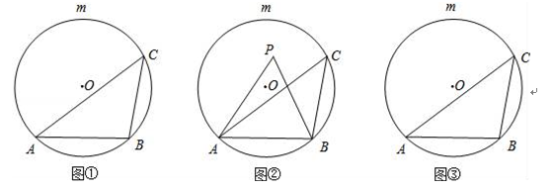
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道:“任何无限循环小数都可以写成分数的形式”.下面给你介绍利用一元一次方程的有关知识来解答这个问题.
问题:利用一元一次方程将
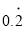 化成分数.
化成分数.解:设
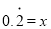 ,
,方程两边同时乘以10得:
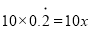 ,
,由
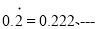 ,得:
,得: 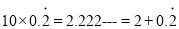 ,
,所以
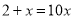 ,
,解得:
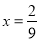 ,即
,即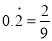 .
.解答下列问题:
(1)填空:将
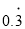 写成分数形式为 ;
写成分数形式为 ;(2)方法归纳:由示例可知:如果循环节为1位时,设方程后两边同时乘以10.那么如果循环节为2位时,设方程后两边同时应乘以 ;
(3)请你仿照上述方法把
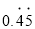 化成分数,要求写出解答过程.
化成分数,要求写出解答过程. -
科目: 来源: 题型:
查看答案和解析>>【题目】在操场上练习双杠的过程中发现双杠的两横杠在地上的影子( )
A.相交
B.互相垂直
C.互相平行
D.无法确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】把数轴上表示数2的点移动3个单位长度后,表示的数为_____
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.b的指数是0
B.b没有系数
C.a是单项式
D.﹣3是一次单项式 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线y=2x﹣5经过点A(a,1﹣a),则A点落在第_____象限.
相关试题

