Question

【题目】如图1，P（2，2），点A在x轴正半轴上运动，点B在y轴上运动，且PA=PB．

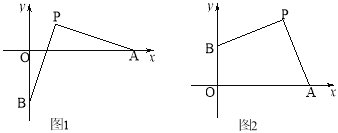
（1）求证：PA⊥PB；

（2）若点A（8，0），求点B的坐标；

（3）求OA – OB的值；

（4）如图2，若点B在y轴正半轴上运动时，直接写出OA+OB的值．

Answer 1

【答案】（1）详见解析；（2）点B的坐标为（0，-4）；（3）4；（4）4．

【解析】

试题分析：（1）过点P作PE⊥x轴于E，作PF⊥y轴于F，根据点P的坐标可得PE=PF=2，然后利用“HL”证明Rt△APE和Rt△BPF全等，根据全等三角形对应角相等可得∠APE=∠BPF，然后求出∠APB=∠EPF=90°，再根据垂直的定义证明；（2）求出AE的长度，再根据全等三角形对应边相等可得AE=BF，然后求出OB，再写出点B的坐标即可；（3）根据全等三角形对应边相等可得PE=PF，再表示出PE、PF，然后列出方程整理即可得解；（4）同（3）的思路求解即可．

试题解析：（1）如图1，过点P作PE⊥x轴于E，作PF⊥y轴于F

∵ P（2，2）

∴ PE=PF=2，∠EPF=90°

在Rt△APE和Rt△BPF中

∴ Rt△APE≌Rt△BPF（HL）

∴ ∠APE=∠BPF

∴ ∠APB=∠APE+∠BPE=∠BPF+∠BPE=90°

∴ PA⊥PB

（2）∵P（2，2）

∴ OE=OF=2

∵ A（8，0）

∴ OA=8

∴ AE=OA-OE=8-2=6

又由⑴得Rt△APE≌Rt△BPF

∴ BF=AE=6

∴ OB=BF-OF=6-2=4

∴ 点B的坐标为（0，-4）

（3）∵ Rt△APE≌Rt△BPF

∴ AE=BF

∵ AE=OA-OE=OA-2

BF=OF+OB= 2 +OB

∴ OA-2= 2 +OB

∴ OA -OB= 4

（4）OA +OB=4