【题目】证明命题“角的平分线上的点到角的两边的距离相等”,要根据题意,画出图形,并用符号表示已知和求证,写出证明过程,下面是小明同学根据题意画出的图形,并写出了不完整的已知和求证.
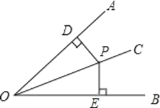
已知:如图,OC是∠AOB的角平分线,点 P 在 OC 上, 求证: .
(要求:请你补全已知和求证,并写出证明过程.)
参考答案:
【答案】PD⊥OA于D,PE⊥OB于E,PD=PE.证明见解析.
【解析】
根据题意、结合图形写出已知和求证,证明△OPD≌△OPE,根据全等三角形的性质即可得到结论.
已知:如图,OC是∠AOB的角平分线,点P在OC上,PD⊥OA于D,PE⊥OB于E,求证:PD=PE.
证明:∵PD⊥OA,PE⊥OB,
∴∠PDO=∠PEO=90°,
∵OC是∠AOB的角平分线,
∴∠AOC=∠BOC
在△PDO和△PEO中,
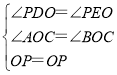 ,
,
∴△PDO≌△PEO(AAS),
∴PD=PE.
故答案为:PD⊥OA于D,PE⊥OB于E,PD=PE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某同学准备购买笔和本子送给农村希望小学的同学,在市场上了解到某种本子的单价比某种笔的单价少4元,且用30元买这种本子的数量与用50元买这种笔的数量相同.
(1)求这种笔和本子的单价;
(2)该同学打算用自己的100元压岁钱购买这种笔和本子,计划100元刚好用完,并且笔和本子都买,请列出所有购买方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】红富士苹果某箱上标明苹果质量为
 ,则这箱苹果最重为__________kg,如果某箱苹果重14.95kg,则这箱苹果_________________标准.(填“符合”或“不符合”)
,则这箱苹果最重为__________kg,如果某箱苹果重14.95kg,则这箱苹果_________________标准.(填“符合”或“不符合”) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A(10,0),以OA为直径在第一象限内作半圆C,点B是该半圆周上的一动点,连结OB、AB,并延长AB至点D,使DB=AB,过点D作x轴垂线,分别交x轴、直线OB于点E、F,点E为垂足,连结CF.

(1)当∠AOB=30°时,求弧AB的长;
(2)当DE=8时,求线段EF的长;
(3)在点B运动过程中,是否存在以点E、C、F为顶点的三角形与△AOB相似,若存在,请求出此时点E的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(问题提出)
学习了三角形全等的判定方法(即“SAS”、“ASA”、“AAS”、“SSS”)和直角三角形全等的判定方法(即“HL”)后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
(初步思考)
我们不妨将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,然后,对∠B进行分类,可分为“∠B是直角、钝角、锐角”三种情况进行探究.

(深入探究)
第一种情况:当∠B是直角时,△ABC≌△DEF.
(1)如图①,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E=90°,根据 ,可以知道Rt△ABC≌Rt△DEF.
第二种情况:当∠B是钝角时,△ABC≌△DEF.
(2)如图②,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是钝角,求证:△ABC≌△DEF.
第三种情况:当∠B是锐角时,△ABC和△DEF不一定全等.
(3)在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是锐角,请你用尺规在图③中作出△DEF,使△DEF和△ABC不全等.(不写作法,保留作图痕迹)
(4)∠B还要满足什么条件,就可以使△ABC≌△DEF?请直接写出结论:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是锐角,若 ,则△ABC≌△DEF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A,B是反比例函数y=
 (k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C,过P作PM⊥x轴,垂足为M.设三角形OMP的面积为S,P点运动时间为t,则S关于x的函数图象大致为( )
(k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C,过P作PM⊥x轴,垂足为M.设三角形OMP的面积为S,P点运动时间为t,则S关于x的函数图象大致为( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1) -2+7-16+9
(2)7-(-3)+(-5)-|-8|
(3)

(4)

(5)(-8)÷(-4)-(-3)3×(-1
 )
) (6)

(7)
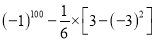
(8)
 ÷
÷
相关试题

