搜索
【题目】计算：
（1） －2＋7－16＋9
（2）7－(－3)＋(－5)－|－8|
（3）
（4）
（5）(－8)÷(－4)－(－3)3×（－1
）
（6）
（7）
（8）
÷
参考答案：
【答案】（1）
（2）
（3）
（4）
（5）
（6）
（7）
（8）
【解析】
（1）先将减法变成加法，然后相加即可得；
（2）先计算绝对值、将减法转化为加法，再计算加减即可得；
（3）利用加法结合律即可得；
（4）先将除法变乘法，然后根据乘法分配律即可得；
（5）先计算乘方，再算乘除即可得；
（6）先计算乘方，再算乘除即可得；
（7）先计算乘方，再算括号里面的，最后算加减即可得；
（8）先计算乘方，然后将除法转化为乘法，再计算即可；
（1）
（2）
（3）
（4）
（5）
（6）
（7）
（8）
-
科目： 来源： 题型：
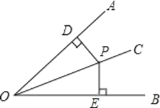
查看答案和解析>>【题目】证明命题“角的平分线上的点到角的两边的距离相等”，要根据题意，画出图形，并用符号表示已知和求证，写出证明过程，下面是小明同学根据题意画出的图形，并写出了不完整的已知和求证．
已知：如图，OC是∠AOB的角平分线，点 P 在 OC 上， 求证： ．
（要求：请你补全已知和求证，并写出证明过程．）
-
科目： 来源： 题型：
查看答案和解析>>【题目】（问题提出）
学习了三角形全等的判定方法（即“SAS”、“ASA”、“AAS”、“SSS”）和直角三角形全等的判定方法（即“HL”）后，我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究．
（初步思考）
我们不妨将问题用符号语言表示为：在△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E，然后，对∠B进行分类，可分为“∠B是直角、钝角、锐角”三种情况进行探究．
（深入探究）
第一种情况：当∠B是直角时，△ABC≌△DEF．
（1）如图①，在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E=90°，根据 ，可以知道Rt△ABC≌Rt△DEF．
第二种情况：当∠B是钝角时，△ABC≌△DEF．
（2）如图②，在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是钝角，求证：△ABC≌△DEF．
第三种情况：当∠B是锐角时，△ABC和△DEF不一定全等．
（3）在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是锐角，请你用尺规在图③中作出△DEF，使△DEF和△ABC不全等．（不写作法，保留作图痕迹）
（4）∠B还要满足什么条件，就可以使△ABC≌△DEF？请直接写出结论：在△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是锐角，若 ，则△ABC≌△DEF．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知A，B是反比例函数y=
（k＞0，x＞0）图象上的两点，BC∥x轴，交y轴于点C，动点P从坐标原点O出发，沿O→A→B→C（图中“→”所示路线）匀速运动，终点为C，过P作PM⊥x轴，垂足为M．设三角形OMP的面积为S，P点运动时间为t，则S关于x的函数图象大致为（ ）
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知点（－1，y1），（2，y2），（3，y3）在反比例函数
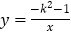的图象上．下列结论中正确的是（ ）A. y1＞y2＞y3 B. y1＞y3＞y2 C. y3＞y1＞y2 D. y2＞y3＞y1
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，半径为1个单位的圆片上有一点A与数轴上的原点重合，AB是圆片的直径．(注：结果保留π )
(1)把圆片沿数轴向右滚动半周，点B到达数轴上点C的位置，点C表示的数是 数(填“无理”或“有理”)，这个数是 ；
(2)把圆片沿数轴滚动2周，点A到达数轴上点D的位置，点D表示的数是 ；
(3)圆片在数轴上向右滚动的周数记为正数，圆片在数轴上向左滚动的周数记为负数，依次运动情况记录如下：+2，﹣1，+3，﹣4，﹣3．
①第 次滚动后，A点距离原点最近，第 次滚动后，A点距离原点最远．
②当圆片结束运动时，A点运动的路程共有 ，此时点A所表示的数是 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】给出下列四个关于是否成反比例的命题，判断它们的真假．
（1）面积一定的等腰三角形的底边长和底边上的高成反比例；
（2）面积一定的菱形的两条对角线长成反比例；
（3）面积一定的矩形的两条对角线长成反比例；
（4）面积一定的直角三角形的两直角边长成比例．
相关试题
