【题目】关于x的方程![]() .
.
(1)求证:无论k为何值,方程总有实数根.
(2)设![]() ,
,![]() 是方程
是方程![]() 的两个根,记S=
的两个根,记S=![]() ,S的值能为2吗?若能,求出此时k的值;若不能,请说明理由.
,S的值能为2吗?若能,求出此时k的值;若不能,请说明理由.
参考答案:
【答案】(1)证明见解析;(2)k=2.
【解析】
试题分析:(1)分两种情况讨论:①当k=1时,方程是一元一次方程,有实数根;②当k≠1时,方程是一元二次方程,所以证明判别式是非负数即可;
(2)由韦达定理得![]() ,
,![]() ,代入到
,代入到![]() =2中,可求得k的值.
=2中,可求得k的值.
试题解析:(1)当k=1时,原方程可化为2x+2=0,解得:x=﹣1,此时该方程有实根;
当k≠1时,方程是一元二次方程,∵△=![]() =
=![]() =
=![]() >0,∴无论k为何实数,方程总有实数根,综上所述,无论k为何实数,方程总有实数根.
>0,∴无论k为何实数,方程总有实数根,综上所述,无论k为何实数,方程总有实数根.
(2)由根与系数关系可知,![]() ,
,![]() ,若S=2,则
,若S=2,则![]() =2,即
=2,即![]() ,将
,将![]() 、
、![]() 代入整理得:
代入整理得:![]() ,解得:k=1(舍)或k=2,∴S的值能为2,此时k=2.
,解得:k=1(舍)或k=2,∴S的值能为2,此时k=2.
-
科目: 来源: 题型:
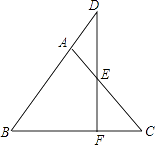
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,E在AC上,且AD=AE,DE的延长线与BC相交于点F.求证:DF⊥BC.
-
科目: 来源: 题型:
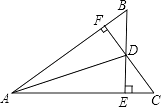
查看答案和解析>>【题目】如图所示,已知BE⊥AC于E,CF⊥AB于F,BE、CF相交于点D,若BF=CE.求证:AD平分∠BAC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙三个游客团的年龄的方差分别是S甲2=1.47,S乙2=10.2,S丙2=2.3,导游小邱最喜欢带游客年龄相近的团队,若在这三个游客团中选择一个,则他应选( )
A. 甲队B. 乙队C. 丙队D. 哪个都可以
-
科目: 来源: 题型:
查看答案和解析>>【题目】气温逐渐升高,甲安装队为A小区安装66台空调,乙安装队为B小区安装60台空调,两队同时开工且恰好同时完工,已知甲队比乙队每天多安装2台,求甲队、乙队每天各安装多少台空调?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知OM平分∠AOC,ON平分∠BOC,∠AOB=90°,∠BOC=30°. 求:
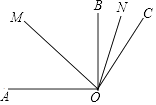
(1)∠AOC的度数;
(2)∠MON的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形每个内角都相等,并且它的一个外角与相邻内角度数的比为2∶7,求这个多边形的边数.
相关试题

