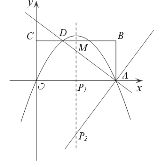
【题目】矩形OABC在平面直角坐标系中的位置如图所示,A、C两点的坐标分别为A(6,0)、C(0,3),直线![]() 与BC边相交于点D.
与BC边相交于点D.

(1)求点D的坐标;
(2)若抛物线![]() 经过A、D两点,试确定此抛物线的解析式;
经过A、D两点,试确定此抛物线的解析式;
(3)设(2)中的抛物线的对称轴与直线AD交于点M,点P为对称轴上一动点,以P、A、M为顶点的三角形与△ABD相似,求符合条件的所有点P的坐标.
参考答案:
【答案】(1)点D的坐标为(2,3);
(2) 抛物线的解析式为![]() ;
;
(3) 符合条件的点P有两个,P1 (3,0)、P2 (3,-4).
【解析】
试题分析:(1)有题目所给信息可以知道,BC线上所有的点的纵坐标都是3,又有D在直线![]() 上,代入后求解可以得出答案.
上,代入后求解可以得出答案.
(2)A、D,两点坐标已知,把它们代入二次函数解析式中,得出两个二元一次方程,联立求解可以得出答案.
(3)由题目分析可以知道∠B=90°,以P、A、M为顶点的三角形与△ABD相似,所以应有∠APM、∠AMP或者∠MAP等于90°,很明显∠AMP不可能等于90°,所以有两种情况.
解:(1) ∵四边形OABC为矩形,C(0,3)
∴BC∥OA,点D的纵坐标为3.
∵直线![]() 与BC边相交于点D,
与BC边相交于点D,
∴![]() . ∴点D的坐标为(2,3).
. ∴点D的坐标为(2,3).
(2) ∵若抛物线![]() 经过A(6,0)、D(2,3)两点,
经过A(6,0)、D(2,3)两点,
∴![]()
解得: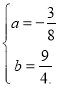 ∴抛物线的解析式为
∴抛物线的解析式为![]()
(3) ∵抛物线![]() 的对称轴为x=3,
的对称轴为x=3,
设对称轴x=3与x轴交于点P1,∴BA∥MP1,
∴∠BAD=∠AMP1.
①∵∠AP1M=∠ABD=90°,∴△ABD∽△AMP1.
∴P1 (3,0).
②当∠MAP2=∠ABD=90°时,△ABD∽△MAP2.
∴∠AP2M=∠ADB
∵AP1=AB,∠AP1 P2=∠ABD=90°
∴△AP1 P2≌△ABD
∴P1 P2=BD=4
∵点P2在第四象限,∴P2 (3,-4).
∴符合条件的点P有两个,P1 (3,0)、P2 (3,-4).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 线段可以比较长短B. 射线可以比较长短
C. 直线可以比较长短D. 直线比射线长
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x=﹣3,y=1,则2x﹣y+1的值为( )
A.6B.4C.﹣3D.﹣6
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,梯形的上底长是5 cm,下底长是11 cm.当梯形的高由大变小时,梯形的面积也随之发生变化.
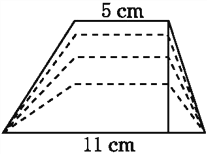
(1)在这个变化过程中,自变量是____________,因变量是____________;
(2)梯形的面积y(cm2)与高x(cm)之间的关系式为____________;
(3)当梯形的高由10 cm变化到1 cm时,梯形的面积由____________变化到____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】到圆心的距离大于半径的点的集合是( )
A.圆的内部B.圆的外部
C.圆D.圆的外部和圆
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三角形ABC中,底边BC=8 cm,高AD=6 cm,点E为AD上一动点,当点E从点D附近向点A运动时,三角形BEC的面积发生了变化.
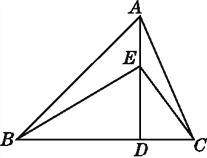
(1)在这个变化过程中,哪些量是变量?哪些量是常量?
(2)如果设DE的长为x cm,三角形BEC的面积为y cm2,那么怎样用含x的式子表示y?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,CD是AB边上的中线,∠B=45,tan∠ACB=3,AC=
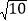 .求:
.求:(1)△ABC的面积;(2)sin∠ACD的值.
相关试题

