【题目】小明骑单车上学,当他骑了一段路时起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校以下是他本次上学所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是 米,本次上学途中,小明一共行驶了 米;
(2)小明在书店停留了 分钟,本次上学,小明一共用了 分钟;
(3)在整个上学的途中那个时间段小明骑车速度最快,最快的速度是多少?

参考答案:
【答案】(1)1500,2700;(2)4,14;(3)在整个上学的途中 从12分钟到14分钟小明骑车速度最快,最快的速度是 450 米/分.
【解析】
(1)因为![]() 轴表示路程,起点是家,终点是学校,故小明家到学校的路程是1500米;共行驶的路程
轴表示路程,起点是家,终点是学校,故小明家到学校的路程是1500米;共行驶的路程![]() 小明家到学校的距离
小明家到学校的距离![]() 折回书店的路程
折回书店的路程![]() .
.
(2)与![]() 轴平行的线段表示路程没有变化,观察图象分析其对应时间即可.
轴平行的线段表示路程没有变化,观察图象分析其对应时间即可.
(3)观察图象分析每一时段所行路程,然后计算出各时段的速度进行比较即可.
解:(1)![]() 轴表示路程,起点是家,终点是学校,
轴表示路程,起点是家,终点是学校,
![]() 小明家到学校的路程是1500米.
小明家到学校的路程是1500米.
![]() (米
(米![]()
即:本次上学途中,小明一共行驶了2700米.
(2)由图象可知:小明在书店停留了4分钟.本次上学,小明一共用了14分钟;
(3)折回之前的速度![]() (米
(米![]() 分),
分),
折回书店时的速度![]() (米
(米![]() 分),
分),
从书店到学校的速度![]() (米
(米![]() 分),
分),
经过比较可知:小明在从书店到学校的时候速度最快,
即:在整个上学的途中从12分钟到14分钟小明骑车速度最快,最快的速度是450米![]() 分.
分.
故答案是:(1)1500,2700;(2)4,14.
-
科目: 来源: 题型:
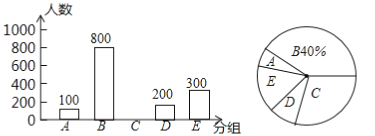
查看答案和解析>>【题目】为调查市民上班时最常用的交通工具的情况,随机抽取了四市部分市民进行调查,要求被调查者从“A:自行车,B:电动车,C:公交车,D:家庭汽车,E:其他”五个选项中选择最常用的一项,将所有调查结果整理后绘制成如下不完整的条形统计图和扇形统计图,请结合统计图回答下列问题:
(1)在这次调查中,一共调查了 名市民.
(2)扇形统计图中,C组对应的扇形圆心角是 .
(3)请补全条形统计图.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上点A,B分别对应数a,b.其中a<0,b>0.
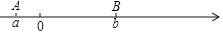
(1)当a=﹣2,b=6时,求a-b=_____,线段AB的中点对应的数是 ;(直接填结果)
(2)若该数轴上另有一点M对应着数m.
①当a=﹣4,b=8,点M在A,B之间,且AM=3BM时,求m的值.
②当m=2,b>2,且AM=2BM时,求代数式a+2b+20的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校要从小王和小李两名同学中挑选一人参加全市知识竞赛,在最近的五次选拔测试中,他俩的成绩分别如下表:
次数
1
2
3
4
5
小王
60
75
100
90
75
小李
70
90
100
80
80
根据上表解答下列问题:
(1)完成下表:
姓名
平均成绩(分)
中位数(分)
众数(分)
方差
小王
80
75
75
190
小李
(2)在这五次测试中,成绩比较稳定的同学是谁?若将80分以上(含80分)的成绩视为优秀,则小王、小李在这五次测试中的优秀率各是多少?
(3)历届比赛表明,成绩达到80分以上(含80分)就很可能获奖,成绩达到90分以上(含90分)就很可能获得一等奖,那么你认为选谁参加比赛比较合适?说明你的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某景区的三个景点A、B、C在同一线路上.甲、乙两名游客从景点A出发,甲步行到景点C;乙乘景区观光车先到景点B,在B处停留一段时间后,再步行到景点C,甲、乙两人同时到达景点C.甲、乙两人距景点A的路程y(米)与甲出发的时间x(分)之间的函数图象如图所示.
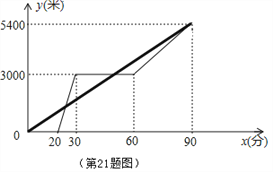
(1)乙步行的速度为_ __米/分.
(2)求乙乘景区观光车时y与x之间的函数关系式.
(3)甲出发多长时间与乙第一次相遇?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某风景区计划在绿化区域种植银杏树,现甲、乙两家有相同的银杏树苗可供选择,其具体销售方案如下:
甲
乙
购树苗数量
销售单价
购树苗数量
销售单价
不超过500棵时
800元/棵
不超过1000棵时
800元/棵
超过500棵的部分
700元/棵
超过1000棵的部分
600元/棵
设购买银杏树苗x棵,到两家购买所需费用分别为y甲元、y乙元
(1)该风景区需要购买800棵银杏树苗,若都在甲家购买所要费用为 元,若都在乙家购买所需费用为 元;
(2)当x>1000时,分别求出y甲、y乙与x之间的函数关系式;
(3)如果你是该风景区的负责人,购买树苗时有什么方案,为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】【问题原型】如图1,在四边形ABCD中,∠ADC=90°,AB=AC.点E、F分别为AC、BC的中点,连结EF,DE.试说明:DE=EF.
【探究】如图2,在问题原型的条件下,当AC平分∠BAD,∠DEF=90°时,求∠BAD的大小.
【应用】如图3,在问题原型的条件下,当AB=2,且四边形CDEF是菱形时,直接写出四边形ABCD的面积.

相关试题

