【题目】已知正方形ABCD的边长为1,点P为正方形内一动点,若点M在AB上,且满足△PBC∽△PAM,延长BP交AD于点N,连结CM.

(1)如图一,若点M在线段AB上,求证:AP⊥BN;AM=AN;
(2)①如图二,在点P运动过程中,满足△PBC∽△PAM的点M在AB的延长线上时,AP⊥BN和AM=AN是否成立?(不需说明理由)
②是否存在满足条件的点P,使得PC=![]() ?请说明理由.
?请说明理由.
参考答案:
【答案】(1)证明见解析;(2)①仍然成立;②不存在.
【解析】
试题分析:(1)由△PBC∽△PAM,推出∠PAM=∠PBC,由∠PBC+∠PBA=90°,推出∠PAM+∠PBA=90°即可证明AP⊥BN,由△PBC∽△PAM,推出![]() ,由△BAP∽△BNA,推出
,由△BAP∽△BNA,推出![]() ,得到
,得到![]() ,由此即可证明.
,由此即可证明.
(2)①结论仍然成立,证明方法类似(1).②这样的点P不存在.利用反证法证明.假设PC=![]() ,推出矛盾即可.
,推出矛盾即可.
试题解析:(1)证明:如图一中,∵四边形ABCD是正方形,∴AB=BC=CD=AD,∠DAB=∠ABC=∠BCD=∠D=90°,∵△PBC∽△PAM,∴∠PAM=∠PBC,![]() ,∴∠PBC+∠PBA=90°,∴∠PAM+∠PBA=90°,∴∠APB=90°,∴AP⊥BN,∵∠ABP=∠ABN,∠APB=∠BAN=90°,∴△BAP∽△BNA,∴
,∴∠PBC+∠PBA=90°,∴∠PAM+∠PBA=90°,∴∠APB=90°,∴AP⊥BN,∵∠ABP=∠ABN,∠APB=∠BAN=90°,∴△BAP∽△BNA,∴![]() ,∴
,∴![]() ,∵AB=BC,∴AN=AM.
,∵AB=BC,∴AN=AM.
(2)解:①仍然成立,AP⊥BN和AM=AN.
理由如图二中,∵四边形ABCD是正方形,∴AB=BC=CD=AD,∠DAB=∠ABC=∠BCD=∠D=90°,∵△PBC∽△PAM,∴∠PAM=∠PBC,![]() ,∴∠PBC+∠PBA=90°,∴∠PAM+∠PBA=90°,∴∠APB=90°,∴AP⊥BN,∵∠ABP=∠ABN,∠APB=∠BAN=90°,∴△BAP∽△BNA,∴
,∴∠PBC+∠PBA=90°,∴∠PAM+∠PBA=90°,∴∠APB=90°,∴AP⊥BN,∵∠ABP=∠ABN,∠APB=∠BAN=90°,∴△BAP∽△BNA,∴![]() ,∴
,∴![]() ,∵AB=BC,∴AN=AM.
,∵AB=BC,∴AN=AM.
②这样的点P不存在.
理由:假设PC=![]() ,如图三中,以点C为圆心
,如图三中,以点C为圆心![]() 为半径画圆,以AB为直径画圆,CO=
为半径画圆,以AB为直径画圆,CO=![]() =
=![]() >1+
>1+![]() ,∴两个圆外离,∴∠APB<90°,这与AP⊥PB矛盾,∴假设不可能成立,∴满足PC=
,∴两个圆外离,∴∠APB<90°,这与AP⊥PB矛盾,∴假设不可能成立,∴满足PC=![]() 的点P不存在.
的点P不存在.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了节约水资源,某市准备按照居民家庭年用水量实行阶梯水价.水价分档递增,计划使第一档、第二档和第三档的水价分别覆盖全市居民家庭的80%,15%和5%,为合理确定各档之间的界限,随机抽查了该市5万户居民家庭上一年的年用水量(单位:m3),绘制了统计图.如图所示,下面四个推断( )
①年用水量不超过180m3的该市居民家庭按第一档水价交费;
②年用水量超过240m3的该市居民家庭按第三档水价交费;
③该市居民家庭年用水量的中位数在150﹣180之间;
④该市居民家庭年用水量的平均数不超过180.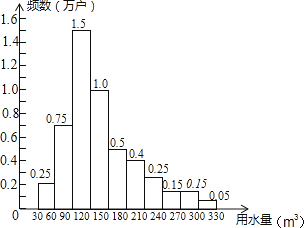
A.①③
B.①④
C.②③
D.②④ -
科目: 来源: 题型:
查看答案和解析>>【题目】绝对值相等且符号不相同的数他们互为。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在正方形ABCD的外侧,作两个等边三角形ADE和DCF,连接AF,BE.
(1)请判断:AF与BE的数量关系是 ,位置关系是 ;
(2)如图2,若将条件“两个等边三角形ADE和DCF”变为“两个等腰三角形ADE和DCF,且EA=ED=FD=FC”,第(1)问中的结论是否仍然成立?请作出判断并给予说明;
(3)若三角形ADE和DCF为一般三角形,且AE=DF,ED=FC,第(1)问中的结论都能成立吗?请直接写出你的判断.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上点A表示的数为8,B是数轴上一点,且AB=14,动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
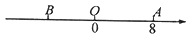
(1)点B表示的数为 , 点P表示的数为(用含t的式子表示);
(2)动点H从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P,H同时出发,问点P运动多少秒时追上点H? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=x2-mx+m-2.(其中m是常数),不论m取何值,抛物线都经过一个定点,则这个定点的坐标为____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将某样本数据分析整理后分成6组,且组距为5,画频数分布折线图时,从左到右第三组的组中值为20.5,则分布两端虚设组组中值为 和 .
相关试题

