【题目】在△ABC和△DEC中,AC=BC,DC=EC,∠ACB=∠ECD=90°.
(1)如图1,当点A、C、D在同一条直线上时,AC=12,EC=5.
①求证:AF⊥BD,
②求AF的长度;
(2)如图2,当点A、C、D不在同一条直线上时.求证:AF⊥BD;
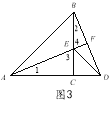
(3)如图3,在(2)的条件下,连接CF并延长CF交AD于点G,∠AFG是一个固定的值吗?若是,求出∠AFG的度数,若不是,请说明理由.

参考答案:
【答案】(1)AF=![]() (2)见解析(3)∠AFG=45°
(2)见解析(3)∠AFG=45°
【解析】
试题分析:(1)①根据SAS可证△ACE≌△BCD,再根据全等三角形的性质可得∠1=∠2,再结合对顶角相等证得结论;
②根据同一个三角形的面积不变可求的AF得值;
(2)如①的方法,根据SAS证得△ACE≌△BCD,再根据全等三角形的性质和垂直的定义可证;
(3)如图4,过点C作CM⊥BD,CN⊥AE,垂足分别为M、N,然后由上面的结论△ACE≌△BCD,可根据全等三角形的面积相等证得CM=CN,再根据角平分线的判定得证CF平分∠BFE,最后根据角平分线的性质得证.
试题解析:(1)①证明:如图1,∵AC=BC,∠ACB=∠ECD=90°,EC=DC,∴△ACE≌△BCD,
∴∠1=∠2,∵∠3=∠4,∴∠BFE=∠ACE=90°,∴AF⊥BD.
②∵∠ECD=90°,BC= AC=12,DC= EC=5,∴BD=13,
∵S△ABD=![]() AD·BC=
AD·BC=![]() BD·AF,∴AF=
BD·AF,∴AF=![]() .
.
(法2:∵∠ECD=90°,BC= AC=12,DC= EC=5,∴AE=BD=13,BE=7,设EF=x,
∵∠BFE=90°,∴BF2=BE2-EF2,BF2=AB2-AF2,∴72-x2=288-(13+x)2,
∴x=![]() ,∴AF=13+
,∴AF=13+![]() =
=![]() .)
.)
(2)证明:如图4,∵∠ACB=∠ECD,∴∠ACB+∠ACD=∠ECD+∠ACD,∴∠BCD=∠ACE,
∵AC=BC,∠ACE=∠BCD,EC=DC,∴△ACE≌△BCD,∴∠1=∠2,
∵∠3=∠4,∴∠BFA=∠BCA=90°,∴AF⊥BD.
(3)∠AFG=45°.
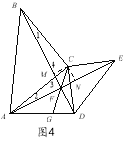
如图4,过点C作CM⊥BD,CN⊥AE,垂足分别为M、N,
∵△ACE≌△BCD,∴S△ACE=S△BCD,AE=BD,∵S△ACE=![]() AE·CN,
AE·CN,
S△BCD=![]() BD·CM,∴CM=CN,
BD·CM,∴CM=CN,
∵CM⊥BD,CN⊥AE,∴CF平分∠BFE,
∵AF⊥BD,∴∠BFE=90°,∴∠EFC=45°,∴∠AFG=45°.
(法2:过点C作CM⊥BD,CN⊥AE,垂足分别为M、N,∵CM⊥BD,CN⊥AE,
∴∠BMC=∠ANC=90°,∵△ACE≌△BCD,∴∠1=∠2,∵∠BMC=∠ANC=90°,∠1=∠2,
AC=BC,∴△BCM≌△ACN,∴CM=CN,∵CM⊥BD,CN⊥AE,∴CF平分∠BFE,
∵AF⊥BD,∴∠BFE=90°,∴∠EFC=45°,∴∠AFG=45°.)
-
科目: 来源: 题型:
查看答案和解析>>【题目】有四张背面相同的纸牌A,B,C,D,其正面分别画有四个不同的几何图形(如图).小华将这四张牌背面朝上洗匀后随机摸出一张,再从剩下的牌中随机的摸出另一张.
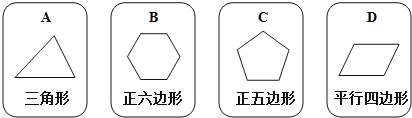
(1)请用树状图(或列表法)表示两次摸牌所有可能的结果;
(2)求摸出两张牌的牌面图形都是中心对称图形的纸牌的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】由等式(a﹣2)x=a﹣2能得到x﹣1=0,则a必须满足的条件是 ________
-
科目: 来源: 题型:
查看答案和解析>>【题目】某大型企业员工总数为28600人,数据“28600”用科学记数法可表示为( )
A. 0.286×105 B. 2.86×105 C. 28.6×103 D. 2.86×104
-
科目: 来源: 题型:
查看答案和解析>>【题目】春天来了天气一天比一天暖和,在同一地点某一物体,今天上午11点的影子比昨天上午11点的影子______.(长,短)
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某校为了创建书香校园,去年购进一批图书.经了解,科普书的单价比文学书的单价多4元,用12000元购进的科普书与用8000元购进的文学书本数相等.
(1)文学书和科普书的单价各多少钱?
(2)今年文学书和科普书的单价和去年相比保持不变,该校打算用10000元再购进一批文学书和科普书,问购进文学书550本后至多还能购进多少本科普书?
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:(a+b)(a﹣b)+(a+b)2﹣2a2,其中a=3,b=﹣1.
相关试题

