【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于C、D两点,DE⊥x轴于点E.已知C点的坐标是(4,-1),DE=2.
的图象交于C、D两点,DE⊥x轴于点E.已知C点的坐标是(4,-1),DE=2.
(1)求反比例函数与一次函数的关系式;
(2)根据图象直接回答:当x为何值时,一次函数的值小于反比例函数的值?

参考答案:
【答案】(1)![]()
![]() ;(2)
;(2) ![]() .
.
【解析】
(1)先由点C的坐标求出反比例函数的关系式,再由DE=2,求出点D的坐标,把点C,点D的坐标代入一次函数关系式求出k,b即可求一次函数的关系式.
(2)由图象可知:一次函数的值小于反比例函数的值.
(1)点C(4,-1)在反比例函数y=![]() 的图象上,
的图象上,
∴m=-4,
∴反比例函数的关系式为y=-![]()
∵点D在反比例函数y=-![]() 上,且DE=2,
上,且DE=2,
∴y=2,代入求得:x=-2,
∴点D的坐标为(-2,2).
∵C、D两点在直线y=kx+b上,
∴![]()
解得: ,
,
∴一次函数的关系式为y=-![]() x+1.
x+1.
(2)由图象可知:当-2<x<0或x>4时,一次函数的值小于反比例函数的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长和宽分别是a,b的长方形的四个角都剪去一个边长为x的正方形,折叠后,做成一无盖的盒子(单位:cm).
(1)用a,b,x表示纸片剩余部分的面积;
(2)用a,b,x表示盒子的体积;
(3)当a=10,b=8且剪去的每一个小正方形的面积等于4 cm2时,求剪去的每一个正方形的边长及所做成的盒子的体积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学数学兴趣小组为了解本校学生对电视节目的喜爱情况,随机调查了部分学生最喜爱哪一类节目(被调查的学生只选一类并且没有不选择的),并将调查结果制成了如下的两个统计图(不完整).请你根据图中所提供的信息,完成下列问题:

(1)本次调查的学生人数为__________,娱乐节目在扇形统计图中所占圆心角的度数是__________度.
(2)请将条形统计图补充完整:
(3)若该中学有2000名学生,请估计该校喜爱动画节目的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=x+m的图象与反比例函数y=
 的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1).
的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1).(1)求m及k的值;
(2)求点C的坐标,并结合图象写出不等式组0<x+m≤
 的解集.
的解集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数轴上点
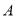 对应的数为
对应的数为  ,点
,点  对应的数为
对应的数为 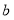 ,且多项式
,且多项式  的二次项系数为
的二次项系数为  ,常数项为
,常数项为 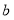 .
.(1)直接写出:
 ,
,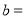 .
.(2)数轴上点
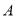 ,
, 之间有一动点
之间有一动点 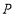 ,若点
,若点 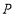 对应的数为
对应的数为 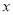 ,试化简
,试化简 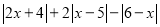 .
.(3)若点
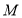 从点
从点 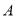 出发,以每秒
出发,以每秒  个单位长度的速度沿数轴向右移动;同时点
个单位长度的速度沿数轴向右移动;同时点 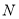 从点
从点  出发,沿数轴以每秒
出发,沿数轴以每秒 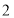 个单位长度的速度向左移动,到达
个单位长度的速度向左移动,到达 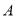 点后立即返回并向右继续移动,经过t秒后,
点后立即返回并向右继续移动,经过t秒后,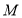 ,
,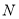 两点相距
两点相距  个单位长度,求t的值.
个单位长度,求t的值. -
科目: 来源: 题型:
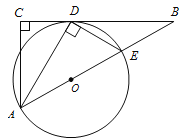
查看答案和解析>>【题目】已知:如图,在△ABC 中,∠C=90°,∠BAC 的平分线 AD 交 BC于点 D,过点 D 作 DE⊥AD 交 AB 于点 E,以 AE 为直径作⊙O.
(1)求证:BC 是⊙O 的切线;
(2)若 AC=3,BC=4,求 BE 的长.
(3)在(2)的条件中,求 cos∠EAD 的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在数学活动课上,将边长为
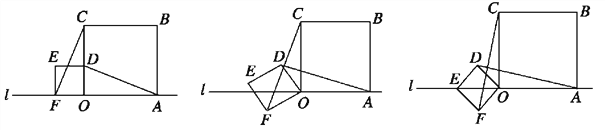
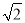 和3的两个正方形放置在直线l上,如图a,他连接AD、CF,经测量发现AD=CF.
和3的两个正方形放置在直线l上,如图a,他连接AD、CF,经测量发现AD=CF.(1)他将正方形ODEF绕O点逆时针针旋转一定的角度,如图b,试判断AD与CF还相等吗?说明理由.
(2)他将正方形ODEF绕O点逆时针旋转,使点E旋转至直线l上,如图c,请求出CF的长.
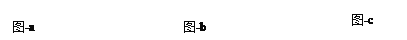
相关试题

