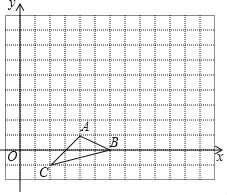
【题目】(1)将△ABC沿x轴负方向平移2个单位,沿y轴正方向平移4个单位,得到△A1B1C1,请画出△A1B1C1.
(2)将△ABC绕点A顺时针旋转90°,得到△AB2C2,请画出△AB2C2.
(3)△A1B1C1绕点P顺时针旋转90°,得到△AB2C2,则点P的坐标为 .
参考答案:
【答案】(1)见解析;(2)见解析;(3)(1,2).
【解析】
(1)找出点A、B、C沿x轴负方向平移2个单位,沿y轴正方向平移4个单位的对应的点A1、B1、C1的位置,然后顺次连接即可得到△A1B1C1;
(2)利用网格特点,找出点A、B、C以点A为旋转中心,顺时针旋转90°后的对应的点A、B2、C2的位置,然后顺次连接即可得到△AB2C2;
(3)任意连接两个对应点,再作出对应点连线的垂直平分线,交点就是旋转中心.
解:(1)如图所示;△A1B1C1即为所求;
(2)如图所示,△AB2C2.即为所求;
(3)∵△A1B1C1绕点P顺时针旋转90°,得到△AB2C2,
∴可作A1A、C1C2的中垂线,交点P即为旋转中心,
∴P点坐标为(1,2).
故答案为:(1,2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在半径为2cm,圆心角为90°的扇形OAB中,分别以OA、OB为直径作半圆,则图中阴影部分的面积为_____.

-
科目: 来源: 题型:
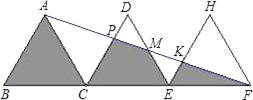
查看答案和解析>>【题目】如图,△ABC、△DCE、△HEF、是三个全等的等边三角形,点B、C、E、F在同一条直线上,连接AF,与DC、DE、HE分别相交于点P、M、K,若△DPM的面积为2,则图中三个阴影部分的面积之和为_____.
-
科目: 来源: 题型:
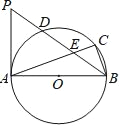
查看答案和解析>>【题目】如图,AB是⊙O的直径,BC为弦,D为弧AC的中点,AC、BD相交于点E.AP交BD的延长线于点P.∠PAC=2∠CBD.
(1)求证:AP是⊙O的切线;
(2)若PD=3,AE=5,求△APE的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,均匀的正四面体的各面依次标有1,2,3,4四个数字.小明做了60次投掷试验,结果统计如下:
朝下数字
1
2
3
4
出现的次数
16
20
14
10
(1)计算上述试验中“4朝下”的频率是 ;
(2)随机投掷正四面体两次,请用列表或画树状图法,求两次朝下的数字之和大于4的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,二次函数y=ax2﹣2ax﹣3a(a<0)的图象与x轴交于A、B两点(点A在点B的右侧),与y轴的正半轴交于点C,顶点为D.
(1)求顶点D的坐标(用含a的代数式表示);
(2)若以AD为直径的圆经过点C.
①求抛物线的函数关系式;
②如图2,点E是y轴负半轴上一点,连接BE,将△OBE绕平面内某一点旋转180°,得到△PMN(点P、M、N分别和点O、B、E对应),并且点M、N都在抛物线上,作MF⊥x轴于点F,若线段MF:BF=1:2,求点M、N的坐标;
③点Q在抛物线的对称轴上,以Q为圆心的圆过A、B两点,并且和直线CD相切,如图3,求点Q的坐标.

-
科目: 来源: 题型:
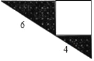
查看答案和解析>>【题目】如图所示是一个直角三角形的苗圃,由一个正方形花坛和两块直角三角形的草皮组成.如果两个直角三角形的两条斜边长分别为4米和6米,则草皮的总面积为( )平方米.
A. 3
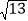 B. 9 C. 12 D. 24
B. 9 C. 12 D. 24
相关试题

