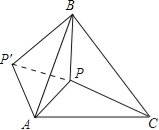
【题目】如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10若将△PAC绕点A逆时针后得到△P′AB.
(1)求点P与点P′之间的距离;
(2)求∠APB的大小.

参考答案:
【答案】(1)6;(2)150°.
【解析】试题分析:(1)由已知△PAC绕点A逆时针旋转后,得到△P′AB,可得△PAC≌△P′AB,PA=P′A,旋转角∠P′AP=∠BAC=60°,所以△APP′为等边三角形,即可求得PP′;
(2)由△APP′为等边三角形,得∠APP′=60°,在△PP′B中,已知三边,用勾股定理逆定理证出直角三角形,得出∠P′PB=90°,可求∠APB的度数.
解:(1)连接PP′,由题意可知BP′=PC=10,AP′=AP,
∠PAC=∠P′AB,而∠PAC+∠BAP=60°,
所以∠PAP′=60度.故△APP′为等边三角形,
所以PP′=AP=AP′=6;
(2)利用勾股定理的逆定理可知:
PP′2+BP2=BP′2,所以△BPP′为直角三角形,且∠BPP′=90°
可求∠APB=90°+60°=150°.
-
科目: 来源: 题型:
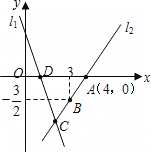
查看答案和解析>>【题目】如图,直线l1的解析表达式为y=-3x+3,且l1与x轴交于点D,直线l2经过点A,B,直线l1,l2,交于点C.
(1)求点D的坐标;
(2)求直线l2的解析表达式;
(3)求△ADC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小颖随机抽样调查本校20名女同学所穿运动鞋尺码,并统计如表:
尺码/cm
21.5
22.0
22.5
23.0
23.5
人数
2
4
3
8
3
学校附近的商店经理根据统计表决定本月多进尺码为23.0cm的女式运动鞋,商店经理的这一决定应用的统计量是( )
A. 平均数 B. 加权平均数 C. 众数 D. 中位数
-
科目: 来源: 题型:
查看答案和解析>>【题目】点(﹣2,6)在正比例函数y=kx图象上,下列各点在此函数图象上的是( )
A.(3,1)B.(﹣3,1)C.(1,3)D.(﹣1,3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】三条线段a=5,b=3,c的值为整数,由a、b、c为边可组成三角形( )
A.1个
B.3个
C.5个
D.无数个 -
科目: 来源: 题型:
查看答案和解析>>【题目】北京某日早晨气温是零下2℃,中午上升了8℃,半夜又下降了6℃,半夜时气温是多少( )
A. ﹣2℃ B. 0℃ C. 2℃ D. 4℃
-
科目: 来源: 题型:
查看答案和解析>>【题目】36.32°=_______°_______′________″.
相关试题

