【题目】如图,△ABC的两条中线AD、CE交于点G,且AD⊥CE.连接BG并延长与AC交于点F,若AD=9,CE=12,则GF为 . 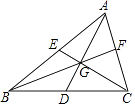
参考答案:
【答案】5
【解析】解:∵点G是△ABC的两条中线AD、CE的交点,
∴点G是△ABC的重心,
∴AG= ![]() AD=6,CG=
AD=6,CG= ![]() CE=8,
CE=8,
∵AD⊥CE,
∴AC= ![]() =10,
=10,
∵点G是△ABC的重心,
∴点F是AC的中点,
∴GF= ![]() AC=5,
AC=5,
所以答案是:5.
【考点精析】解答此题的关键在于理解三角形的“三线”的相关知识,掌握1、三角形角平分线的三条角平分线交于一点(交点在三角形内部,是三角形内切圆的圆心,称为内心);2、三角形中线的三条中线线交于一点(交点在三角形内部,是三角形的几何中心,称为中心);3、三角形的高线是顶点到对边的距离;注意:三角形的中线和角平分线都在三角形内.
-
科目: 来源: 题型:
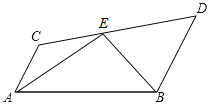
查看答案和解析>>【题目】如图所示,已知AC∥BD,EA,EB分别平分∠CAB和∠DBA,CD过E点.求证:AB=AC+BD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图∠BAC的角平分线与BC的垂直平分线DG交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F.
⑴试说明:BE=CF;
⑵若AF=3,BC=4,求△ABC的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列两则材料:
材料一:我们可以将任意三位数记为
 (其中a,b,c分别表示该数百位数字、十位数字和个位数字,且a≠0),显然
(其中a,b,c分别表示该数百位数字、十位数字和个位数字,且a≠0),显然 =100a+10b+c.
=100a+10b+c.材料二:若一个三位数的百位数字、十位数字和个位数字均不为0,则称之为原始数,比如123就是一个原始数,将原始数的三个数位上的数字交换顺序,可产生出5个原始数,比如由123可以产生出132,213,231,312,321这5个原始数.将这6个数相加,得到的和1332称为由原始数123生成的终止数.利用材料解决下列问题:
(1)分别求出由下列两个原始数生成的终止数:243,537;
(2)若一个原始数
 的终止数是另一个原始数
的终止数是另一个原始数 的终止数的3倍,分别求出所有满足条件的这两个原始数.
的终止数的3倍,分别求出所有满足条件的这两个原始数. -
科目: 来源: 题型:
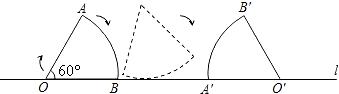
查看答案和解析>>【题目】如图,将半径为3cm,圆心角为60°的扇形纸片.AOB在直线l上向右作无滑动的滚动至扇形A′O′B′处,则顶点O经过的路线总长 cm(结果保留π).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的两条中线AD、CE交于点G,且AD⊥CE.连接BG并延长与AC交于点F,若AD=9,CE=12,则GF为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将半径为3cm,圆心角为60°的扇形纸片.AOB在直线l上向右作无滑动的滚动至扇形A′O′B′处,则顶点O经过的路线总长 cm(结果保留π).
相关试题

