【题目】某中学初一年级有350名同学去春游,已知2辆A型车和1辆B型车可以载学生100人;1辆A型车和2辆B型车可以载学生110人.(1)A、B型车每辆可分别载学生多少人?(2)若租一辆A型车需要1000元,一辆B型车需1200元,请你设计租车方案,使得恰好运送完学生并且租车费用最少.
参考答案:
【答案】(1)每辆A型车可载学生30人,每辆B型车可载学生40人.(2)租1辆A型车、8辆B型车.
【解析】
(1)设每辆A型车可载学生x人,每辆B型车可载学生y人,根据“2辆A型车和1辆B型车可以载学生100人;1辆A型车和2辆B型车可以载学生110人”,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)设租A型车m辆,租B型车n辆,根据总人数=30×租用A型车的数量+40×租用B型车的数量,即可得出关于m,n的二元一次方程,结合m,n均为正整数即可得出各租车方案,利用总钱数=每辆车的租车费用×租车数量可求出各方案所需费用,比较后即可得出结论.
解:(1)设每辆A型车可载学生x人,每辆B型车可载学生y人,
依题意,得:![]() ,
,
解得:![]() .
.
答:每辆A型车可载学生30人,每辆B型车可载学生40人.
(2)设租A型车m辆,租B型车n辆,
依题意,得:30m+40n=350,
解得:m=![]() .
.
∵m,n均为正整数,
∴![]() ,
,![]() ,
,![]() .
.
当m=9,n=2时,租车费用为1000×9+1200×2=11400(元);
当m=5,n=5时,租车费用为1000×5+1200×5=11000(元);
当m=1,n=8时,租车费用为1000×1+1200×8=10600(元).
∵11400>11000>10600,
∴租1辆A型车、8辆B型车.
-
科目: 来源: 题型:
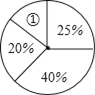
查看答案和解析>>【题目】物理兴趣小组20位同学在实验操作中的得分情况如下表:(Ⅰ)求这组数据的众数、中位数;(Ⅱ)求这组数据的平均数;(Ⅲ)将此次操作得分按人数制成如图所示的扇形统计图.扇形①的圆心角度数是多少?
得分(分)
10
9
8
7
人数(人)
5
8
4
3
-
科目: 来源: 题型:
查看答案和解析>>【题目】经过点(2,0)且与坐标轴围成的三角形面积为2的直线解析式是__________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为保护学生的身体健康,某中学课桌椅的高度都是按一定的关系(一次函数)配套设计的,下表列出5套符合条件的课桌椅的高度. ①假设课桌的高度为ycm椅子的高度为xcm,请确定y与x的函数关系式;②现有一把高37cm的椅子和一张高71.5cm的课桌,它们是否配套?为什么?
椅子高度x(cm)
45
42
39
36
33
桌子高度y(cm)
84
79
74
69
64
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F.
(1)求证:AE=CF.
(2)求证:四边形BFDE为矩形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某社区超市第一次用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的
 倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)甲
乙
进价(元/件)
22
30
售价(元/件)
29
40
(1)该超市购进甲、乙两种商品各多少件?
(2)该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(3)该超市第二次以第一次的进价又购进甲、乙两种商品,其中甲商品的件数不变,乙商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多180元,求第二次乙商品是按原价打几折销售?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰梯形ABCD中,AD∥BC,M、N分别为AD、BC的中点,E、F分别是BM、CM的中点.
⑴求证:△ABM≌△DCM;
⑵四边形MENF是什么图形?请证明你的结论;
⑶若四边形MENF是正方形,则梯形的高与底边BC有何数量关系?并请说明理由.

相关试题

