【题目】如图,DABC中,AB=BC=AC=12cm,现有两点M,N分别从现有两点M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为1cm/s,点N的速度为2cm/s.当点N第一次到达B点时,M、N同时停止运动.
(1)点M、N运动几秒后,M、N两点重合?
(2)点M、N运动几秒后,可得到等边三角形△AMN?
(3)当点M、N在BC边上运动时,能否得到以MN为底边的等腰三角形?如存在,请求出此时M、N运动的时间.
参考答案:
【答案】
(1)解:设点M、N运动x秒后,M、N两点重合,
x×1+12=2x,解得:x=12
(2)解:设点M、N运动t秒后,可得到等边三角形△AMN,如图①,
AM=t×1=t,AN=AB-BN=12-2t,∵三角形△AMN是等边三角形,∴t=12-2t,
解得t=4,∴点M、N运动4秒后,可得到等边三角形△AMN
(3)解:当点M、N在BC边上运动时,可以得到以MN为底边的等腰三角形,
由(1)知12秒时M、N两点重合,恰好在C处,
如图②,
假设△AMN是等腰三角形,∴AN=AM,∴∠AMN=∠ANM,
∴∠AMC=∠ANB,∵AB=BC=AC,∴△ACB是等边三角形,∴∠C=∠B,
在△ACM和△ABN中,
∵  ,∴△ACM≌△ABN,∴CM=BN,
,∴△ACM≌△ABN,∴CM=BN,
设当点M、N在BC边上运动时,M、N运动的时间y秒时,△AMN是等腰三角形,
∴CM=y-12,NB=36-2y,CM=NB,y-12=36-2y,解得:y=16.故假设成立.
∴当点M、N在BC边上运动时,能得到以MN为底边的等腰三角形,此时M、N运动的时间为16秒
【解析】(1)首先设点M、N运动x秒后,M、N两点重合,表示出M,N的运动路程,根据N的运动路程=M的运动路程+12,列出方程求解即可。
(2)根据题意设点M、N运动t秒后,要得到等边三角形△AMN,由于∠A等于60°,只需AM=AN,然后用含t的代数式表示出AM,AN的长,所以根据AM=AN建立方程求解即可。
(3)首先假设△AMN是等腰三角形,可证出△ACM≌△ABN,可得CM=BN,设出运动时间,表示出CM,NB,NM的长,根据CM=NB列出方程,可解出未知数的值即可。
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=3x﹣2的图象上有两点A(﹣1,y1),B(﹣2,y2),则y1与y2的大小关系为( )
A. y1>y2 B. y1<y2 C. y1=y2 D. 不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校实施新课程改革以来,学生的学习能力有了很大提高.王老师为进一步了解本班学生自主学习、合作交流的现状,对该班部分学生进行调查,把调查结果分成四类(A:特别好,B:好,C:一般,D:较差)后,再将调查结果绘制成两幅不完整的统计图(如图).请根据统计图解答下列问题:

(1)本次调查中,王老师一共调查了 名学生;
(2)将条形统计图补充完整;
(3)为了共同进步,王老师从被调查的A类和D类学生中分别选取一名学生进行“兵教兵”互助学习,请用列表或画树状图的方法求出恰好选中一名男生和一名女生的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“成自”高铁自贡仙市段在建设时,甲、乙两个工程队计划参与该项工程建设,甲队单独施工30天完成该项工程的
 ,这时乙队加入,两队还需同时施工30天,才能完成该项工程.
,这时乙队加入,两队还需同时施工30天,才能完成该项工程.
(1)若乙队单独施工,需要多少天才能完成该项工程?
(2)若甲队参与该项工程施工的时间不超过40天,则乙队至少施工多少天才能完成该项工程? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点C在⊙O上,点D在AB延长线上,且∠BCD=∠A.
(1)求证:DC是⊙O的切线;
(2)若∠A=30°,AC=2
 ,求图中阴影部分的面积.
,求图中阴影部分的面积.
-
科目: 来源: 题型:
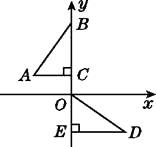
查看答案和解析>>【题目】如图,在平面直角坐标系中,点B,C,E在y轴上,Rt△ABC经过变换得到Rt△ODE,若点C的坐标为(0,1),AC=2,则这种变换可以是( )
A.△ABC绕点C顺时针旋转90°,再向下平移3个单位长度
B.△ABC绕点C顺时针旋转90°,再向下平移1个单位长度
C.△ABC绕点C逆时针旋转90°,再向下平移1个单位长度
D.△ABC绕点C逆时针旋转90°,再向下平移3个单位长度 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△AOB是等腰直角三角形,直线BD∥OA,OB=OA=1,P是线段AB上一动点,过P点作MN∥OB,分别交OA、BD于M、N,PC⊥PO,交BD于点C.
(1)求证:OP=PC;
(2)当点C在射线BN上时,设AP长为m,四边形POBC的面积为S,请求出S与m间的函数关系式,并写出自变量m的取值范围;
(3)当点P在线段AB上移动时,点C也随之在直线BN上移动,△PBC是否可能成为等腰三角形?如果可能,求出所有能使△PBC成为等腰三角形时的PM的值;如果不可能,请说明理由.

相关试题

