【题目】如图,在正方形纸片ABCD中,E,F分别是AD,BC的中点,沿过点B的直线折叠,使点C落在EF上,落点为N,折痕交CD边于点M,BM与EF交于点P,再展开.则下列结论中:①CM=DM;②∠ABN=30°;③AB2=3CM2;④△PMN是等边三角形.
正确的有( )
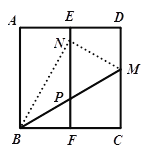
A. 1个B. 2个C. 3个D. 4个
参考答案:
【答案】C
【解析】
∵△BMN是由△BMC翻折得到的,
∴BN=BC,又点F为BC的中点,
在Rt△BNF中,sin∠BNF=![]() ,
,
∴∠BNF=30°,∠FBN=60°,
∴∠ABN=90°-∠FBN=30°,故②正确;
在Rt△BCM中,∠CBM=![]() ∠FBN=30°,
∠FBN=30°,
∴tan∠CBM=tan30°=![]() ,
,
∴BC=![]() CM,AB2=3CM2故③正确;
CM,AB2=3CM2故③正确;
∠NPM=∠BPF=90°-∠MBC=60°,∠NMP=90°-∠MBN=60°,
∴△PMN是等边三角形,故④正确;
由题给条件,证不出CM=DM,故①错误.
故正确的有②③④,共3个.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点 E,F 是ABCD 对角线上两点,在条件①DE=BF;②∠ADE=∠CBF; ③AF=CE;④∠AEB=∠CFD 中,添加一个条件,使四边形 DEBF 是平行四边形,可添加 的条件是( )
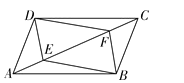
A. ①②③ B. ①②④ C. ①③④ D. ②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了增强学生体质,决定开设以下体育课外活动项目:A.篮球 B.乒乓球C.羽毛球 D.足球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,

请回答下列问题:
(1)这次被调查的学生共有多少人?
(2)请你将条形统计图(2)补充完整;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)
-
科目: 来源: 题型:
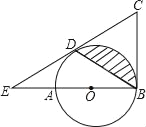
查看答案和解析>>【题目】如图,AB是⊙O的直径,BC是⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E,
(1)求证:CD为⊙O的切线;
(2)若EA=BO=2,求图中阴影部分的面积(结果保留π)
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,AB=15,AC=13,高AD=12,则△ABC的面积为______________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)该玩具销售单价定为多少元时,商场能获得12000元的销售利润?
(2)该玩具销售单价定为多少元时,商场获得的销售利润最大?最大利润是多少?
(3)若玩具厂规定该品牌玩具销售单价不低于46元,且商场要完成不少于500件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A1,A2,A3…和B1,B2,B3,…分别在直线y=
 x+b和x轴上.△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形如果点A1(1,1),那么点A2019的纵坐标是_____.
x+b和x轴上.△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形如果点A1(1,1),那么点A2019的纵坐标是_____.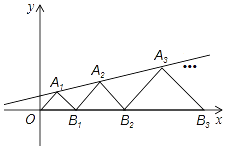
相关试题

