【题目】2013年6月,某中学结合广西中小学阅读素养评估活动,以“我最喜爱的书籍”为主题,对学生最喜爱的一种书籍类型进行随机抽样调查,收集整理数据后,绘制出以下两幅未完成的统计图,请根据图1和图2提供的信息,解答下列问题:
(1)在这次抽样调查中,一共调查了多少名学生?
(2)请把折线统计图(图1)补充完整;
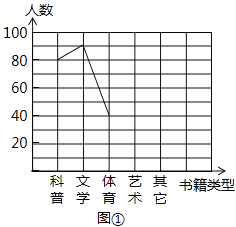
(3)求出扇形统计图(图2)中,体育部分所对应的圆心角的度数;

(4)如果这所中学共有学生1800名,那么请你估计最喜爱科普类书籍的学生人数.
参考答案:
【答案】解:(1)∵90÷30%=300(名),
∴一共调查了300名学生。
(2)艺术的人数:300×20%=60名,其它的人数:300×10%=30名。
补全折线图如下:
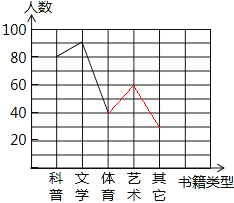
(3)体育部分所对应的圆心角的度数为:![]() ×360°=48°。
×360°=48°。
(4)∵1800×![]() =480(名),
=480(名),
∴1800名学生中估计最喜爱科普类书籍的学生人数为480。
【解析】
试题(1)用文学的人数除以所占的百分比计算即可得解。
(2)根据所占的百分比求出艺术和其它的人数,然后补全折线图即可。
(3)用体育所占的百分比乘以360°,计算即可得解。
(4)用总人数乘以科普所占的百分比,计算即可得解。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某项工程如果由乙单独完成比甲单独完成多用6天;如果甲、乙先合做4天后,再由乙单独完成,那么乙一共所用的天数刚好和甲单独完成工程所用的天数相等.
(1)求甲单独完成全部工程所用的时间;
(2)该工程规定须在20天内完成,若甲队每天的工程费用是4.5万元,乙队每天的工程费用是2.5万元,请你选择上述一种施工方案,既能按时完工,又能使工程费用最少,并说明理由?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知线段AB=4,延长AB到点C,使得AB=2BC,反向延长AB到点D,使AC=2AD.
(1)求线段CD的长;
(2)若Q为AB的中点,P为线段CD上一点,且BP=
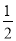 BC,求线段PQ的长.
BC,求线段PQ的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,射线OA的方向是北偏东15°,射线OB的方向是北偏西40°,∠AOB=∠AOC,射线OD是OB的反向延长线.
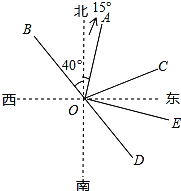
(1)射线OC的方向是 ;
(2)若射线OE平分∠COD,求∠AOE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】张老师元旦节期间到武商众圆商场购买一台某品牌笔记本电脑,恰逢商场正推出“迎元旦”促销打折活动,具体优惠情况如表:
购物总金额(原价)
折扣
不超过5000元的部分
九折
超过5000元且不超过10000元的部分
八折
超过10000元且不超过20000元的部分
七折
……
……
例如:若购买的商品原价为15000元,实际付款金额为:
5000×90%+(10000﹣5000)×80%+(15000﹣10000)×70%=12000元.
(1)若这种品牌电脑的原价为8000元/台,请求出张老师实际付款金额;
(2)已知张老师购买一台该品牌电脑实际付费5700元.
①求该品牌电脑的原价是多少元/台?
②若售出这台电脑商场仍可获利14%,求这种品牌电脑的进价为多少元/台?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
社会消费品零售总额是指批发和零售业,住宿和餐饮业以及其他行业直接售给城乡居民和社会集团的消费品零售额,在各类与消费有关的统计数据中,社会消费品零售总额是表现国内消费需求最直接的数据.
2012年,北京市全年实现社会消费品零售总额7702.8亿元,比上一年增长11.6%,2013年,全年实现社会消费品零售总额8375.1亿元,比上一年增长8.7%,2014年,全年实现社会消费品零售总额9098.1亿元,比上一年增长8.6%,2015年,全年实现社会消费品零售总额10338亿元,比上一年增长7.3%.
2016年,北京市实现市场总消费19926.2亿元,比上一年增长了8.1%,其中实现服务性消费8921.1亿元,增长10.1%;实现社会消费品零售总额11005.1亿元,比上一年增长了6.5%.
根据以上材料解答下列问题:
(1)补全统计表:
2012﹣2016年北京市社会消费品零售总额统计表
年份
2012年
2013年
2014年
2015年
2016年
社会消费品零售总额(单位:亿元)
____
_____
_____
_____
_____
(2)选择适当的统计图将2012﹣2016年北京市社会消费品零售总额比上一年的增长率表示出来,并在图中表明相应数据;
(3)根据以上信息,估计2017年北京市社会消费品零售总额比上一年的增长率约为_________,你的预估理由是_________________.
-
科目: 来源: 题型:
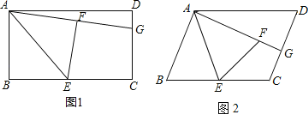
查看答案和解析>>【题目】(1)操作发现:如图1,在矩形ABCD中,E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在矩形ABCD内部,延长AF交CD于点G.猜想线段GF与GC有何数量关系?并证明你的结论.
(2)简单应用:在(1)中,如果AB=4,AD=6,求DG的长;
(3)类比探究:如图2,将(1)中的矩形ABCD改为平行四边形,其它条件不变,(1)中的结论是否仍然成立?请说明理由.
相关试题

