【题目】已知函数f(x)=mex+x+1. (Ⅰ)讨论f(x)的单调性;
(Ⅱ)若f(x)有两个零点x1 , x2(x1<x2),证明:x1+x2>0.
参考答案:
【答案】(Ⅰ)解:f′(x)=mex+1, m≥0时,f′(x)>0,f(x)在R递增,
m<0时,令f′(x)>0,解得:x<ln(﹣ ![]() ),
),
令f′(x)<0,解得:x>ln(﹣ ![]() ),
),
故f(x)在(﹣∞,ln(﹣ ![]() ))递增,在(ln(﹣
))递增,在(ln(﹣ ![]() ),+∞)递减;
),+∞)递减;
(Ⅱ)证明:若f(x)有两个零点x1 , x2(x1<x2),
由(Ⅰ)得:f(x)max=f(ln(﹣ ![]() ))=ln(﹣
))=ln(﹣ ![]() )>0,
)>0,
解得:﹣1<m<0,
由f(x1)=f(x2)得:m= ![]() ①,
①,
m( ![]() ﹣
﹣ ![]() )+(x1﹣x2)=0②,
)+(x1﹣x2)=0②,
将①代入②整理得:
x1= ![]() +1,
+1,
故x2+x1= ![]() +1+x2 ,
+1+x2 ,
由m= ![]() =
= ![]() 得:﹣1<
得:﹣1< ![]() <0,
<0,
解得:﹣1<x2<0,
令g(x)= ![]() +x+1,(﹣1<x<0),
+x+1,(﹣1<x<0),
则g′(x)=1﹣xe﹣x>0,
故g(x)在(﹣1,0)递增,
g(x)>g(﹣1)=0,
故x2+x1= ![]() +1+x2>0.
+1+x2>0.
【解析】(Ⅰ)求出函数的导数,通过讨论a的范围,求出函数的单调区间即可;(Ⅱ)求出x2+x1= ![]() +1+x2 , 由m=
+1+x2 , 由m= ![]() =
= ![]() ,解得:﹣1<x2<0,令g(x)=
,解得:﹣1<x2<0,令g(x)= ![]() +x+1,(﹣1<x<0),根据函数的单调性证明即可.
+x+1,(﹣1<x<0),根据函数的单调性证明即可.
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD与等边△PAD所在的平面相互垂直,AD=2,∠DAB=60°.

(Ⅰ)证明:AD⊥PB;
(Ⅱ)求三棱锥C﹣PAB的高. -
科目: 来源: 题型:
查看答案和解析>>【题目】为丰富人民群众业余生活,某市拟建设一座江滨公园,通过专家评审筛选出建设方案A和B向社会公开征集意见.有关部门用简单随机抽样方法调查了500名市民对这两种方案的看法,结果用条形图表示如下:

(Ⅰ)根据已知条件完成下面的2×2列联表,并用独立性检验的方法分析,能否在犯错误的概率不超过0.01的前提下认为是否选择方案A和年龄段有关?选择方案A
选择方案B
总计
老年人
非老年人
总计
500
附:
(Ⅱ)根据(Ⅰ)的结论,能否提出一个更好的调查方法,使得调查结果更具代表性,说明理由.P(K2≥k)
0.100
0.050
0.010
0.001
k
2.706
3.841
6.635
10.828
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线C:y2=4x的焦点为F,准线为l.⊙F与C交于A,B两点,与x轴的负半轴交于点P. (Ⅰ)若⊙F被l所截得的弦长为
 ,求|AB|;
,求|AB|;
(Ⅱ)判断直线PA与C的交点个数,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系xOy中,曲线C1的方程为
 .以坐标原点为极点,以x轴的正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为ρ2﹣8ρsinθ+15=0. (Ⅰ)写出C1的参数方程和C2的直角坐标方程;
.以坐标原点为极点,以x轴的正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为ρ2﹣8ρsinθ+15=0. (Ⅰ)写出C1的参数方程和C2的直角坐标方程;
(Ⅱ)设点P在C1上,点Q在C2上,求|PQ|的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设不等式|x﹣4|﹣|2x﹣7|>
 (x﹣7)的解集为M.
(x﹣7)的解集为M.
(1)求M;
(2)证明:当a、b∈M时,|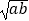 ﹣2|<|2
﹣2|<|2  ﹣
﹣  |.
|. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级数学模拟测试中,六名学生的数学成绩如下(单位:分):110,106,109,111,108,110,下列关于这组数据描述正确的是( )
A.众数是110
B.方差是16
C.平均数是109.5
D.极差是6
相关试题

