【题目】蚂蚁从点O出发,在一条直线上来回爬行.假定向右爬行的路程记为正数,向左爬行的路程记为负数,则爬过的各段路程依次记为(单位:cm):+5,-3,+10,-8,-6,+12,-10.
![]()
(1)蚂蚁最后是否回到出发点O?
(2)蚂蚁离开出发点O最远是多少?
(3)在爬行过程中,如果每爬行1奖励一粒糖,那么蚂蚁一共得到多少粒糖?
参考答案:
【答案】(1)回到了出发点;(2)12cm;(3)54粒
【解析】试题分析:(1)要想知道蚂蚁是否能回到原点,关键是看它分别向左向右的爬行路程之和是否为0.
(2)离出发点最远的距离,就是将小虫爬行的路程依次相加,看看走到哪一段是最大值.
(3)要求一共得到多少米粒,即就是问蚂蚁一共爬行了多少路程即可.
解:(1)将所有记录的路程相加,得
(+5)+(-3)+(+10)+(-8)+(-6)+(+12)+(-10)
=((+5)+(+10)+(+12))+((-3)+(-8)+(-6)+(-10))
=27+(-27)
=0(cm).
即左右爬行的路程相同, 蚂蚁最后回到出发点O.
(2)根据记录的数据,得
蚂蚁离出发点最远的距离是(+5)+(-3)+(+10)=12(cm).
(3)取所有路程的绝对值,得
|+5|+|3|+|+10|+|8|+|6|+|+12|+|10|
=5+3+10+8+6+12+10
=54(cm).
由于每爬行1cm,奖励一粒糖,所以蚂蚁一共得到芝麻的粒数为:54×1=54(粒).
答: 蚂蚁一共得到54粒糖.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016湖北襄阳第23题)
襄阳市某企业积极响应政府“创新发展”的号召,研发了一种新产品.已知研发、生产这种产品的成本为30元/件,且年销售量y(万件)关于售价x(元/件)的函数解析式为:

(1)若企业销售该产品获得自睥利润为W(万元),请直接写出年利润W(万元)关于售价(元/件)的函数解析式;
(2)当该产品的售价x(元/件)为多少时,企业销售该产品获得的年利润最大?最大年利润是多少?
(3)若企业销售该产品的年利澜不少于750万元,试确定该产品的售价x(元/件)的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法错误的是( )
A. 必然发生的事件发生的概率为1
B. 不可能发生的事件发生的概率为0
C. 随机事件发生的概率大于0且小于1
D. 概率很小的事件不可能发生
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
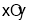 中,直线
中,直线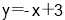 与
与 轴交于点
轴交于点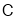 ,与直线
,与直线 交于点
交于点 ,点
,点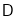 的坐标为
的坐标为
(1)求直线
 的解析式;
的解析式;(2)直线
 与
与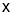 轴交于点
轴交于点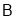 ,若点
,若点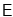 是直线
是直线 上一动点(不与点
上一动点(不与点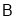 重合),当
重合),当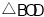 与
与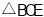 相似时,求点
相似时,求点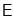 的坐标
的坐标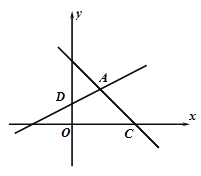
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知某种植物花粉的直径为0.000035米,那么用科学记数法可表示为( )
A.3.5×104米
B.3.5×10﹣4米
C.3.5×10﹣5米
D.3.5×105米 -
科目: 来源: 题型:
查看答案和解析>>【题目】点(﹣1,y1)、(2,y2)是直线y=﹣2x+1上的两点,则y1y2(填“>”或“=”或“<”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.a3a4=a12
B.(a3)4=a12
C.(a2b)3=a5b3
D.a3÷a4=a
相关试题

