搜索
【题目】方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，点C的坐标为（4，﹣1）．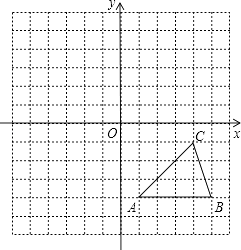
（1）试作出△ABC以C为旋转中心，沿顺时针方向旋转90°后的图形△A1B1C；
（2）以原点O为对称中心，再画出与△ABC关于原点O对称的△A2B2C2 ， 并写出点C2的坐标．
参考答案：
【答案】
（1）
解：根据旋转中心为点C，旋转方向为顺时针，旋转角度为90°，
所作图形如下：
．
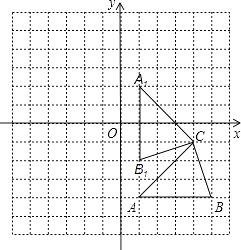（2）
解：所作图形如下：
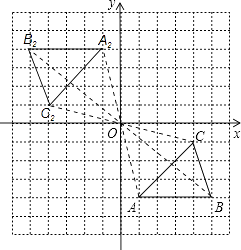
结合图形可得点C2坐标为（﹣4，1）
【解析】（1）根据题意所述的旋转三要素，依此找到各点旋转后的对应点，顺次连接可得出△A1B1C；（2）根据中心对称点平分对应点连线，可找到各点的对应点，顺次连接可得△A2B2C2 ， 结合直角坐标系可得出点C2的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图①，在△ABC中，∠BAC=90°，AB=AC，点E在AC上（且不与点A，C重合），在△ABC的外部作△CED，使∠CED=90°，DE=CE，连接AD，分别以AB，AD为邻边作平行四边形ABFD，连接AF．
（1）请直接写出线段AF，AE的数量关系 ；
（2）将△CED绕点C逆时针旋转，当点E在线段BC上时，如图②，连接AE，请判断线段AF，AE的数量关系，并证明你的结论；
（3）在图②的基础上，将△CED绕点C继续逆时针旋转，请判断（2）问中的结论是否发生变化？若不变，结合图③写出证明过程；若变化，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在一个不透明的口袋中，装有若干个红球和4个黄球，它们除颜色外没有任何区别，摇匀后从中随机摸出一个球，记下颜色后再放回口袋中，通过大量重复摸球实验发现，摸到黄球的频率是0.2，则估计盒子中大约有红球（ ）
A.16个
B.20个
C.25个
D.30个 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，圆M经过原点O，直线
与x轴、y轴分别相交于A，B两点．
（1）求出A，B两点的坐标；
（2）若有一抛物线的对称轴平行于y轴且经过点M，顶点C在圆M上，开口向下，且经过点B，求此抛物线的函数解析式；
（3）设（2）中的抛物线交
轴于D、E两点，在抛物线上是否存在点P，使得S△PDE=
S△ABC？若存在，请求出点P的坐标；若不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】若|2x-1|=7，则|5x+7|=______．
-
科目： 来源： 题型：
查看答案和解析>>【题目】若x2+y2=10，xy=﹣3，则（x+y）2=_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】南京地铁三号线全长为44830米，将44830用科学记数法表示为 ．
相关试题
