【题目】已知:如图,在平面直角坐标系xOy中,直线AB与x轴交于点A(-2,0),与反比例函数在第一象限内的图象的交于点B(2,n),连结BO,若S△AOB=4.

(1)求该反比例函数的解析式和直线AB的解析式;
(2)若直线AB与y轴的交点为C,求△OCB的面积.
参考答案:
【答案】(1)反比例函数的解析式为:y=![]() ;直线AB的解析式为y=x+2;(2)
;直线AB的解析式为y=x+2;(2)
【解析】
试题分析:(1)先由A(-2,0),得OA=2,点B(2,n),S△AOB=4,得![]() OAn=4,n=4,则点B的坐标是(2,4),把点B(2,4)代入反比例函数的解析式为y=
OAn=4,n=4,则点B的坐标是(2,4),把点B(2,4)代入反比例函数的解析式为y=![]() ,可得反比例函数的解析式为:y=
,可得反比例函数的解析式为:y=![]() ;再把A(-2,0)、B(2,4)代入直线AB的解析式为y=kx+b可得直线AB的解析式为y=x+2.
;再把A(-2,0)、B(2,4)代入直线AB的解析式为y=kx+b可得直线AB的解析式为y=x+2.
(2)把x=0代入直线AB的解析式y=x+2得y=2,即OC=2,可得S△OCB=![]() OC×2=
OC×2=![]() ×2×2=2.
×2×2=2.
试题解析:(1)由A(-2,0),得OA=2;
∵点B(2,n)在第一象限内,S△AOB=4,
∴![]() OAn=4;
OAn=4;
∴n=4;
∴点B的坐标是(2,4);
设该反比例函数的解析式为y=![]() (a≠0),
(a≠0),
将点B的坐标代入,得4=![]() ,
,
∴a=8;
∴反比例函数的解析式为:y=![]() ;
;
设直线AB的解析式为y=kx+b(k≠0),
将点A,B的坐标分别代入,得
![]() ,
,
解得
![]() ;
;
∴直线AB的解析式为y=x+2;
(2)在y=x+2中,令x=0,得y=2.
∴点C的坐标是(0,2),
∴OC=2;
∴S△OCB=![]() OC×2=
OC×2=![]() ×2×2=2.
×2×2=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中, ∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB于点E,AB=18cm,则△DBE的周长为( )
A. 16cm B. 8cm C. 18cm D. 10cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】若|x+1|+(y﹣2)2=0,则x+y=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A、B、C三点在同一条直线上,如果线段AB=3cm,BC=1cm,那么A、C两点间的距离为( )
A. 4cm B. 2cm C. 4cm或2cm D. 不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,真命题是( )
A. 相等的圆心角所对的弧相等
B. 面积相等的两个圆是等圆
C. 三角形的内心到各顶点的距离相等
D. 长度相等的弧是等弧
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个正数的两个平方根分别是2a+1和a﹣4,则a的值是 .
-
科目: 来源: 题型:
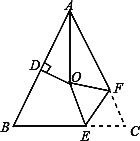
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠BAC=64°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC为_________度.
相关试题

