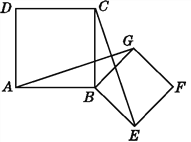
【题目】如图,四边形ABCD,四边形BEFG均为正方形,连接AG,CE.试说明:
(1)AG=CE;
(2)AG⊥CE.
参考答案:
【答案】(1)答案见解析;(2)答案见解析
【解析】试题分析:(1)由正方形的性质有AB=CB,∠ABC=∠GBE=90°,BG=BE,进而得出∠ABG=∠CBE,由SAS证明△ABG≌△CBE,得出对应边相等即可;
(2)由△ABG≌△CBE,得出对应角相等∠BAG=∠BCE,由∠BAG+∠AMB=90°,对顶角∠AMB=∠CMN,得出∠BCE+∠CMN=90°,证出∠CNM=90°即可.
试题解析:证明:(1)∵四边形ABCD、BEFG均为正方形,∴AB=CB,∠ABC=∠GBE=90°,BG=BE,∴∠ABG=∠CBE.
在△ABG和△CBE中,∵AB=CB,∠ABG=∠CBE,BG=BE,∴△ABG≌△CBE(SAS),∴AG=CE;
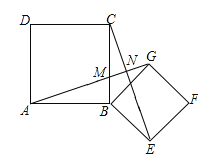
(2)如图所示:∵△ABG≌△CBE,∴∠BAG=∠BCE.
∵∠ABC=90°,∴∠BAG+∠AMB=90°.
∵∠AMB=∠CMN,∴∠BCE+∠CMN=90°,∴∠CNM=90°,∴AG⊥CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个数的偶次幂是正数,这个数是( )
A.正数
B.负数
C.正数或负数
D.任何有理数 -
科目: 来源: 题型:
查看答案和解析>>【题目】一个两位数,十位上的数字为a,个位上的数字为b,这个两位数为( )
A.ab
B.a+b
C.10a+b
D.10ab -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC和△ADE都是等腰三角形,且∠BAC=90°,∠DAE=90°,B,C,D在同一条直线上.求证:BD=CE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】 因式分解:x3-6x2+9x=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:2a3+8a2b+8ab2=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形、等边三角形、矩形、正方形和圆这五个图形中,既是轴对称图形又是中心对称图形的个数是__.
相关试题

