【题目】已知:△ABC是边长为4的等边三角形,点O在边AB上,⊙O过点B且分别与边AB,BC相交于点D,E,EF⊥AC,垂足为F.
(1)求证:直线EF是⊙O的切线;
(2)当直线DF与⊙O相切时,求⊙O的半径.

参考答案:
【答案】(1)证明见解析(2)![]()
【解析】试题分析:(1)连接![]() 欲证直线
欲证直线![]() 是
是![]() 的切线,只需证明
的切线,只需证明![]() .利用等边三角形的三个内角都是60°、等腰
.利用等边三角形的三个内角都是60°、等腰![]() 以及三角形的内角和定理求得同位角
以及三角形的内角和定理求得同位角![]() 从而判定
从而判定![]() ,所以由已知条件
,所以由已知条件![]() 判定
判定![]() 即直线
即直线![]() 是
是![]() 的切线;
的切线;
(2)连接![]() 设
设![]() 的半径是
的半径是![]() .由等边三角形的三个内角都是60°、三条边都相等、以及在直角三角形中30°所对的直角边是斜边的一半求得关于
.由等边三角形的三个内角都是60°、三条边都相等、以及在直角三角形中30°所对的直角边是斜边的一半求得关于![]() 的方程
的方程![]() ,解方程即可.
,解方程即可.
试题解析:(1)证明:连接![]()
![]() 是等边三角形,
是等边三角形,
![]()
在![]() 中,
中,![]()
![]()
![]()
![]() (同位角相等,两直线平行);
(同位角相等,两直线平行);
![]()
![]() 即直线
即直线![]() 是
是![]() 的切线;
的切线;
(2)连接![]()
![]() 与
与![]() 相切,
相切,
![]()
设![]() 的半径是
的半径是![]() ,则
,则![]()
在![]() 中,
中,![]()
![]()
![]()
在![]() 中,
中,![]()
![]()
解得,![]()
![]() 的半径是
的半径是![]()

-
科目: 来源: 题型:
查看答案和解析>>【题目】作图题:如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣1,4),C(﹣3,2).
(1)画出△ABC关于y轴对称的图形△A1B1C1,并直接写出C1点坐标;
(2)以原点O为位似中心,位似比为1:2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2,并直接写出C2点坐标;
(3)如果点D(a,b)在线段AB上,请直接写出经过(2)的变化后D的对应点D2的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
 ,试分别根据下列条件,求出点
,试分别根据下列条件,求出点 的坐标.
的坐标.(1)点
 在
在 轴上;
轴上;(2)点
 的纵坐标比横坐标大3;
的纵坐标比横坐标大3;(3)点
 到
到 轴的距离为2,且在第四象限.
轴的距离为2,且在第四象限. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,已知
中,已知 ,动点
,动点 同时从
同时从 两点出 发,分别沿
两点出 发,分别沿 方向匀速移动,动点
方向匀速移动,动点 的速度是
的速度是 ,动点
,动点 的速度是
的速度是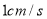 ,当点
,当点 到达点
到达点 时,
时,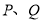 两点停止运动,连接
两点停止运动,连接 ,设点
,设点 的运动时间为
的运动时间为 ,试解答下面的问题:
,试解答下面的问题:  当
当 时,求
时,求 的面积?
的面积?  当
当 为何值时,点
为何值时,点 在线段
在线段 的垂直平分线上?
的垂直平分线上?  是否存在某一时刻
是否存在某一时刻 ,使点
,使点 在
在 的角平分线上,若存在,请求出
的角平分线上,若存在,请求出 的值;若不存 在,请说明理由?
的值;若不存 在,请说明理由?  请用含有
请用含有 的代数式表示四边形
的代数式表示四边形 的面积.
的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:四边形ABCD中,AB=2,CD=3,M、N分别是AD,BC的中点,则线段MN的取值范围是( )

A. 1<MN<5 B. 1<MN≤5 C.
 <MN<
<MN< D.
D.  <MN≤
<MN≤
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形
 中,
中,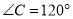 ,
,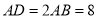 ,点
,点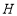 、
、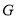 分别是边
分别是边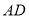 、
、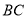 上的动点.连接
上的动点.连接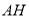 、
、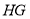 ,点
,点 为
为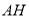 的中点,点
的中点,点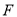 为
为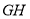 的中点,连接
的中点,连接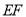 .则
.则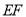 的最大值与最小值的差为( )
的最大值与最小值的差为( )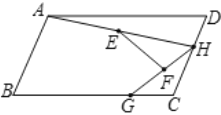
A.2B.
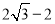 C.
C.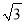 D.
D.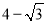
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地区在一次九年级数学做了检测中,有一道满分8分的解答题,按评分标准,所有考生的得分只有四种:0分,3分,5分,8分.老师为了了解学生的得分情况与题目的难易情况,从全区4500名考生的试卷中随机抽取一部分,通过分析与整理,绘制了如下两幅图不完整的统计图.
请根据以上信息解答下列问题:
(1)填空:a= ,b= ,并把条形统计图补全;
(2)请估计该地区此题得满分(即8分)的学生人数;
(3)已知难度系数的计算公式为L=
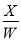 ,其中L为难度系数,X为样本平均得分,W为试题满分值.一般来说,根据试题的难度系数可将试题分为以下三类:当0<L≤0.4时,此题为难题;当0.4<L≤0.7时,此题为中等难度试题;当0.7<L<1时,此题为容易题.试问此题对于该地区的九年级学生来说属于哪一类?
,其中L为难度系数,X为样本平均得分,W为试题满分值.一般来说,根据试题的难度系数可将试题分为以下三类:当0<L≤0.4时,此题为难题;当0.4<L≤0.7时,此题为中等难度试题;当0.7<L<1时,此题为容易题.试问此题对于该地区的九年级学生来说属于哪一类?
相关试题

