【题目】如图,在![]() 中,已知
中,已知![]() ,动点
,动点![]() 同时从
同时从![]() 两点出 发,分别沿
两点出 发,分别沿![]() 方向匀速移动,动点
方向匀速移动,动点![]() 的速度是
的速度是![]() ,动点
,动点![]() 的速度是
的速度是![]() ,当点
,当点![]() 到达点
到达点![]() 时,
时,![]() 两点停止运动,连接
两点停止运动,连接![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]() ,试解答下面的问题:
,试解答下面的问题:
![]() 当
当![]() 时,求
时,求![]() 的面积?
的面积?
![]() 当
当![]() 为何值时,点
为何值时,点![]() 在线段
在线段![]() 的垂直平分线上?
的垂直平分线上?
![]() 是否存在某一时刻
是否存在某一时刻![]() ,使点
,使点![]() 在
在![]() 的角平分线上,若存在,请求出
的角平分线上,若存在,请求出![]() 的值;若不存 在,请说明理由?
的值;若不存 在,请说明理由?
![]() 请用含有
请用含有![]() 的代数式表示四边形
的代数式表示四边形![]() 的面积.
的面积.

参考答案:
【答案】(1)![]() ;(2)t=4;(3)不存在,理由见详解;(4)
;(2)t=4;(3)不存在,理由见详解;(4)![]() .
.
【解析】
(1)根据题意可知当t=1时,AP=2cm,据此过P作PM垂直于BC,进行分析求出![]() 的面积即可;
的面积即可;
(2)由题意可知B在PQ的垂直平分线上即BP=BQ, 设t=m,,则有BP=12-2m, BQ=m,进而进行分析求解即可;
(3)根据题意可知Q在![]() 的平分线上,设CQ为n,AQ为2n,分别求出CQ和BQ,以及当
的平分线上,设CQ为n,AQ为2n,分别求出CQ和BQ,以及当![]() 时,Q在
时,Q在![]() 的平分线上, 比较AP和BP的大小即可;
的平分线上, 比较AP和BP的大小即可;
(4)根据题意连接AQ,并过P作PD垂直于BC,利用![]() 进行分析即可.
进行分析即可.
解:(1)∵在![]() 中,已知
中,已知![]() ,
,
∴AB=12cm,BC= ![]() cm,
cm,
当t=1时,AP=2cm,
∴![]() ,
,![]() ,
,
过P作PM垂直于BC,
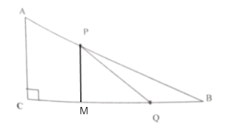
则有![]()
![]() ,
,
∴![]()
![]() .
.
(2)B在PQ的垂直平分线上即BP=BQ,
设t=m,如下图,
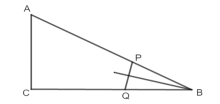
则有BP=12-2m, BQ=m,得出12-2m=m,解得m=4,
∴t=4时,点![]() 在线段
在线段![]() 的垂直平分线上.
的垂直平分线上.
(3)Q在![]() 的平分线上,如图,
的平分线上,如图,
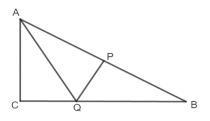
∵![]()
![]()
∴![]() ,
,
∴![]() ,
,
设CQ为n,AQ为2n,则有![]() ,解得n=
,解得n=![]() 或-
或-![]() (舍去),
(舍去),
∴![]()
∴当![]() 时,Q在
时,Q在![]() 的平分线上,此时
的平分线上,此时![]() ,
,
∵![]()
∴不存在某一时刻![]() ,使点
,使点![]() 在
在![]() 的角平分线上.
的角平分线上.
(4)连接AQ,如下图,
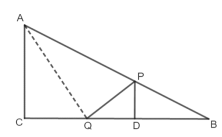
![]() ,
,
过P作PD垂直于BC,如上图,
则有![]() ,
,![]()
∴![]()
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读理解下面的例题,再按要求解答下列问题: 同学们,我们把学习新的数学知识的时候,经常利用“化归“的数学思想方法解决问题,比如,我们在学习二元一次方程组的解法时,是通过“消元”的方法将二元方程化归成我们所 熟悉的一元方程,从而正确求解.下面我们就利用“化归”的数学方法解决新的问题. 首先,我们把像这样,只含有一个未知数,并且未知教的最高次数是
 的不等式,称为一元二次不等式.通过以前的学习,我们已经认识了一无一次不等式、一元一次不等式组并掌握 了它们的解法.同学们,你们能类比一元一次不等式(组)的解法求出一元二次不等式的解 集吗? 例题:解一元二次不等式
的不等式,称为一元二次不等式.通过以前的学习,我们已经认识了一无一次不等式、一元一次不等式组并掌握 了它们的解法.同学们,你们能类比一元一次不等式(组)的解法求出一元二次不等式的解 集吗? 例题:解一元二次不等式 为了解决这个问题,我们需要将一元二次不等式“化归”到一元一次不等式(组),通过平方差公式的逆用,我们可以把
为了解决这个问题,我们需要将一元二次不等式“化归”到一元一次不等式(组),通过平方差公式的逆用,我们可以把 写成
写成 的形式,从面将
的形式,从面将 转化为
转化为 ,然后再利用两数相乘的符号性质将一元二次不等式转化成一元一次不等式(组),从而解决问题.
,然后再利用两数相乘的符号性质将一元二次不等式转化成一元一次不等式(组),从而解决问题.解:

 可化为
可化为
由有理数的乘法法则“两数相乘,同号得正”,得①
 ②
②
解不等式组①,
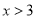
解不等式组②,

即一元二次不等式
 的解集为
的解集为
拓展应用:
 求一元二次不等式
求一元二次不等式 的解集.
的解集. 求分式不等式
求分式不等式 的解集.
的解集. 求一元二次不等式
求一元二次不等式 的解集.
的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】作图题:如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣1,4),C(﹣3,2).
(1)画出△ABC关于y轴对称的图形△A1B1C1,并直接写出C1点坐标;
(2)以原点O为位似中心,位似比为1:2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2,并直接写出C2点坐标;
(3)如果点D(a,b)在线段AB上,请直接写出经过(2)的变化后D的对应点D2的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
 ,试分别根据下列条件,求出点
,试分别根据下列条件,求出点 的坐标.
的坐标.(1)点
 在
在 轴上;
轴上;(2)点
 的纵坐标比横坐标大3;
的纵坐标比横坐标大3;(3)点
 到
到 轴的距离为2,且在第四象限.
轴的距离为2,且在第四象限. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:△ABC是边长为4的等边三角形,点O在边AB上,⊙O过点B且分别与边AB,BC相交于点D,E,EF⊥AC,垂足为F.
(1)求证:直线EF是⊙O的切线;
(2)当直线DF与⊙O相切时,求⊙O的半径.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:四边形ABCD中,AB=2,CD=3,M、N分别是AD,BC的中点,则线段MN的取值范围是( )

A. 1<MN<5 B. 1<MN≤5 C.
 <MN<
<MN< D.
D.  <MN≤
<MN≤
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形
 中,
中,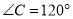 ,
,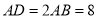 ,点
,点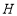 、
、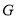 分别是边
分别是边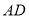 、
、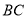 上的动点.连接
上的动点.连接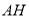 、
、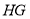 ,点
,点 为
为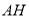 的中点,点
的中点,点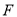 为
为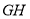 的中点,连接
的中点,连接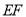 .则
.则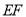 的最大值与最小值的差为( )
的最大值与最小值的差为( )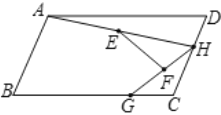
A.2B.
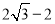 C.
C.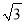 D.
D.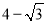
相关试题

