【题目】901班的全体同学根据自己的兴趣爱好参加了六个学生社团(每个学生必须参加且只参加一个),为了了解学生参加社团的情况,学生会对该班参加各个社团的人数进行了统计,绘制成了如图不完整的扇形统计图,已知参加“读书社”的学生有15人,请解答下列问题:
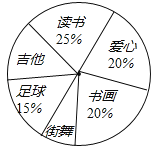
(1)该班的学生共有 名;
(2)若该班参加“吉他社”与“街舞社”的人数相同,请你计算,“吉他社”对应扇形的圆心角的度数;
(3)901班学生甲、乙、丙是“爱心社”的优秀社员,现要从这三名学生中随机选两名学生参加“社区义工”活动,请你用画树状图或列表的方法求出恰好选中甲和乙的概率.
参考答案:
【答案】(1)60;(2)36°;(3)![]() .
.
【解析】试题(1)利用参加“读书社”的学生数除以所占比例进而求出总人数;
(2)首先求出参加“吉他社”的学生在全班学生中所占比例,进而求出对应扇形的圆心角的度数;
(3)首先画出树状图,进而求出恰好选中甲和乙的概率.
试题解析:(1)∵参加“读书社”的学生有15人,且在扇形统计图中,所占比例为:25%,∴该班的学生共有:15÷25%=60(人);故答案为:60;
(2)参加“吉他社”的学生在全班学生中所占比例为: ![]() =10%,所以,“吉他社”对应扇形的圆心角的度数为:360°×10%=36°;
=10%,所以,“吉他社”对应扇形的圆心角的度数为:360°×10%=36°;
(3)画树状图如下:
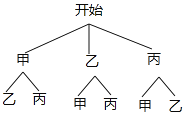 ,
,
由树状图可知,共有6种可能的情况,其中恰好选中甲和乙的情况有2种,故P(选中甲和乙)=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】兴趣小组的同学要测量树的高度.在阳光下,一名同学测得一根长为
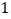 米的竹竿的影长为
米的竹竿的影长为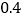 米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为
米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为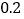 米,一级台阶高为
米,一级台阶高为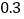 米,如图所示,若此时落在地面上的影长为
米,如图所示,若此时落在地面上的影长为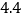 米,则树高为( )
米,则树高为( )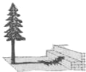
A. 11.5米 B. 11.75米 C. 11.8米 D. 12.25米
-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)如图,AC是ABCD的一条对角线,过AC中点O的直线分别交AD,BC于点E,F.
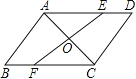
(1)求证:△AOE≌△COF;
(2)当EF与AC满足什么条件时,四边形AFCE是菱形?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一艘渔船以30海里/h的速度由西向东追赶鱼群.在A处测得小岛C在船的北偏东60°方向;40min后渔船行至B处,此时测得小岛C在船的北偏东
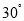 方向.问:小岛C于渔船的航行方向的距离是________________海里(结果可用带根号的数表示).
方向.问:小岛C于渔船的航行方向的距离是________________海里(结果可用带根号的数表示).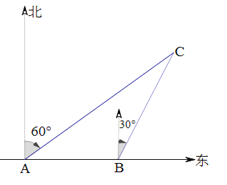
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2017甘肃省天水市)△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合,将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,线段EF与射线CA相交于点Q.
(1)如图①,当点Q在线段AC上,且AP=AQ时,求证:△BPE≌△CQE;
(2)如图②,当点Q在线段CA的延长线上时,求证:△BPE∽△CEQ;并求当BP=2,CQ=9时BC的长.

-
科目: 来源: 题型:
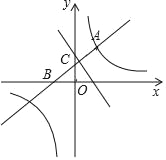
查看答案和解析>>【题目】如图,直线y=x+b与双曲线y=
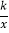 (k是常数,k≠0)在第一象限内交于点A(1,2),且与x轴、y轴分别交于B,C两点.点P在x轴.
(k是常数,k≠0)在第一象限内交于点A(1,2),且与x轴、y轴分别交于B,C两点.点P在x轴.(1)求直线和双曲线的解析式;
(2)若△BCP的面积等于2,求P点的坐标;
(3)求PA+PC的最短距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,CF⊥AB于点F,BE⊥AC于点E,M为BC的中点连接ME、MF、EF.
(1) 求证:△MEF是等腰三角形;
(2) 若∠A=
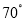 ,∠ABC=50°,求∠EMF的度数.
,∠ABC=50°,求∠EMF的度数.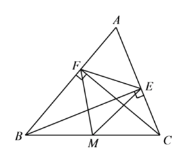
相关试题

