【题目】如图,在△ABC中,∠BAC=90°,AB=AC,AD是经过A点的一条直线,且B、C在AD的两侧,BD⊥AD于D,CE⊥AD于E,交AB于点F,CE=10,BD=4,则DE的长为( )

A. 6 B. 5 C. 4 D. 8
参考答案:
【答案】A
【解析】
根据∠BAC=90°,AB=AC,得到∠BAD+∠CAD=90°,由于CE⊥AD于E,于是得到∠ACE+∠CAE=90°,根据余角的性质得到∠BAD=∠ACE,推出△ABD≌△CEA,根据全等三角形的性质即可得到结论.
解:∵∠BAC=90°,AB=AC,
∴∠BAD+∠CAD=90°,
∵CE⊥AD于E,
∴∠ACE+∠CAE=90°,
∴∠BAD=∠ACE,
在△ABD与△ACE中,
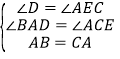 ,
,
∴△ABD≌△CEA(AAS),
∴AE=BD=4,AD=CE=10,
∴DE=AD﹣AE=6.
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明从家骑自行车出发,沿一条直路到相距2400m的邮局办事,小明出发的同时,他的爸爸以96m/min速度从邮局同一条道路步行回家,小明在邮局停留2min后沿原路以原速返回,设他们出发后经过t min时,小明与家之间的距离为s1m,小明爸爸与家之间的距离为s2m,图中折线OABD、线段EF分别表示s1、s2与t之间的函数关系的图象.

(1)求s2与t之间的函数关系式;
(2)小明从家出发,经过多长时间在返回途中追上爸爸?这时他们距离家还有多远?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,设点B的横坐标为x,点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )

A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,直线AB∥CD,点P在两平行线之间,写出∠BAP、∠APC、∠DCP满足的数量关系.
(2)如图2,直线AB与CD相交于点E,点P为∠AEC内一点,AQ平分∠EAP,CQ平分∠ECP,若∠AEC=40°,∠AQC=70°,求∠APC的度数.
(3)如图3,连接AD、CB交于点P,AQ平分∠BAD,CQ平分∠BCD,探究∠ABC、∠AQC、∠ADC满足的关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.

(1)求证:DE=DF;
(2)若∠A=60°,BE=1,求△ABC的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB∥CD,∠B=90°,AB=AD=5,BC=4,M、N、E分别是AB、AD、CB上的点,AM=CE=1,AN=3,点P从点M出发,以每秒1个单位长度的速度沿折线MB﹣BE向点E运动,同时点Q从点N出发,以相同的速度沿折线ND﹣DC﹣CE向点E运动,当其中一个点到达后,另一个点也停止运动.设△APQ的面积为S,运动时间为t秒,则S与t函数关系的大致图象为( )

A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,点A,B分别在x轴,y轴上,点A的坐标为(﹣1,0),∠ABO=30°,线段PQ的端点P从点O出发,沿△OBA的边按O→B→A→O运动一周,同时另一端点Q随之在x轴的非负半轴上运动,如果PQ=
 ,那么当点P运动一周时,点Q运动的总路程为 .
,那么当点P运动一周时,点Q运动的总路程为 . 
相关试题

