Question

【题目】（1）如图1，直线AB∥CD，点P在两平行线之间，写出∠BAP、∠APC、∠DCP满足的数量关系．

（2）如图2，直线AB与CD相交于点E，点P为∠AEC内一点，AQ平分∠EAP，CQ平分∠ECP，若∠AEC=40°，∠AQC=70°，求∠APC的度数．

（3）如图3，连接AD、CB交于点P，AQ平分∠BAD，CQ平分∠BCD，探究∠ABC、∠AQC、∠ADC满足的关系．

Answer 1

【答案】（1）∠BAP+∠DCP=∠APC；（2）100°；（3）∠ABC+∠ADC=2∠AQC.

【解析】

（1）过P作PE∥AB，利用平行线的性质：两直线平行内错角相等，易得到∠BAP、∠APC、∠DCP间关系；

（2）连接EQ并延长至G，连接QP并延长到H，利用角平分线的性质和三角形的外角等于不相邻的两个内角的关系，先得到∠QAP+∠QCP=30°，再得到∠APC的度数．

（3）利用角平分线的性质，得到∠BAQ=∠QAD，∠DCQ=∠QCB，利用三角形的外角等于不相邻的两个内角，通过∠BEQ、∠DFQ把∠ABC、∠AQC、∠ADC、连接起来得到结论.

解:（1）如图1所示，过P作PE∥AB，

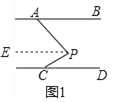
∵AB∥CD，∴PE∥CD

∵PE∥AB，∴∠BAP=∠APE，

同理，∠DCP=∠CPE

∴∠BAP+∠DCP=∠APE+∠CPE=∠APC

故答案为：∠BAP+∠DCP=∠APC，

（2）连接EQ并延长至G，

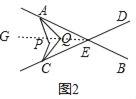
∵AQ平分∠EAP，CQ平分∠ECP，

∴∠EAQ=∠QAP，∠ECQ=∠QCP

∵∠AQG=∠QAE+∠AEQ，∠CQG=∠QCE+∠CEQ，

∴∠AQG+∠CQG=∠QAE+∠AEQ+∠QCE+∠CEQ，

即∠AQC=∠CEA+∠QAE+∠QCE

∵∠AEC=40°，∠AQC=70°

∴∠QAE+∠QCE=30°

即∠QAP+∠QCP=30°

连接QP并延长到H．

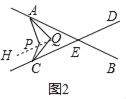
∵∠APH=∠AQP+∠PAQ，∠CPH=∠PQC+∠PCQ，

∴∠APH+∠CPH=∠AQP+∠PAQ+∠PQC+∠PCQ，

即∠APC=∠CQA+∠QAP+∠QCP

∴∠APC=30°+70°=100°．

（3）如图3中，

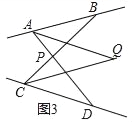
∵AQ平分∠BAD，CQ平分∠BCD，

∴∠BAQ=∠QAD，∠DCQ=∠QCB

∵∠BEQ=∠ABC+∠BAQ=∠BCQ+∠AQC，

∵∠QFD=∠ADC+∠QCD=∠QAD+∠AQC，

∴∠ABC+∠BAQ+∠ADC+∠QCD=∠BCQ+∠AQC+∠QAD+∠AQC

即∠ABC+∠ADC=2∠AQC.