【题目】如图1,在正方形ABCD中,E,F,G,H分别为边AB,BC,CD,DA上的点,HA=EB=FC=GD,连接EG,FH,交点为O.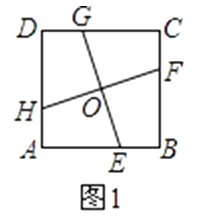
(1)如图1,连接GH,GF,求证:GH=GF;
(2)如图2,连接EF,FG,GH,HE,试判断四边形EFGH的形状,并证明你的结论;
(3)将正方形ABCD沿线段EG,HF剪开,再把得到的四个四边形按图3的方式拼接成一个四边形.若正方形ABCD的边长为3cm,HA=EB=FC=GD=1cm,则图3中阴影部分的面积为cm2 . (直接写结果)
参考答案:
【答案】
(1)证明:∵四边形EFGH是正方形. ∴∠C=∠D=90°,AB=BC=CD=DA, ∵HA=EB=FC=GD,
∴AE=BF=CG=DH, ∴△CGF≌△DHG ∴ GH=GF;
(2)证明:∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA,
∵HA=EB=FC=GD,
∴AE=BF=CG=DH,
∴△AEH≌△BFE≌△CGF≌△DHG,
∴EF=FG=GH=HE,
∴四边形EFGH是菱形,
∵△DHG≌△AEH,
∴∠DHG=∠AEH,
∵∠AEH+∠AHE=90°,
∴∠DHG+∠AHE=90°,
∴∠GHE=90°,
∴四边形EFGH是正方形
(3)解:S阴影=1. ∵HA=EB=FC=GD=1,AB=BC=CD=AD=3, ∴GF=EF=EH=GH= ![]() ,
,
∵由(1)知,四边形EFGH是正方形, ∴GO=OF,∠GOF=90°, 由勾股定理得:GO=OF= ![]() ,
,
∵S四边形FCGO= ![]() ×1×2+
×1×2+ ![]() ×
× ![]() ×
× ![]() =
= ![]() , ∴S阴影=
, ∴S阴影= ![]() ﹣S四边形FCGO×4=10﹣9=1
﹣S四边形FCGO×4=10﹣9=1
【解析】(1)根据正方形的性质得出∠C=∠D=90°,AB=BC=CD=DA, 结合已知得出AE=BF=CG=DH,从而判断出△CGF≌△DHG,根据全等三角形的性质得出结论;
(2)根据正方形的性质得出∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA, 结合已知得出AE=BF=CG=DH,从而推出△AEH≌△BFE≌△CGF≌△DHG,由全等三角形的性质得出EF=FG=GH=HE,进而判断出四边形EFGH是菱形,再找出∠GHE=90°,根据正方形的判定得出四边形EFGH是正方形;
(3)根据已知条件,知道重新拼出来的图形是正方形,利用勾股定理求出GF,GO,FO的长,从而求出阴影部分的面积。
【考点精析】掌握勾股定理的概念是解答本题的根本,需要知道直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形中有一个内角为40°,则其底角的度数是_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为解决“最后一公里一的交通接驳同题,苏州市投放了大量公租自行车供 市民使用到2014年底,全市已有公租自行车25 000辆,租赁点600个,预计到2016年底,全市将有公租自行车50 000辆,并且平均每个租赁点的公租自行车数量是2014年底平均每个租赁点的公租自行车数量的1.2倍,预计到2016年底,全市将有租赁点多少个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】近年来,我国多个城市遭遇雾霾天气,空气中可吸入颗粒(又称PM2.5)浓度升高,为应对空气污染,小强家购买了空气净化器,该装置可随时显示室内PM2.5的浓度,并在PM2.5浓度超过正常值25(mg/m3)时吸收PM2.5以净化空气.随着空气变化的图象(如图),请根据图象,解答下列问题:

(1)写出点M的实际意义;
(2)求第1小时内,y与t的一次函数表达式;
(3)已知第5﹣6小时是小强妈妈做晚餐的时间,厨房内油烟导致PM2.5浓度升高.若该净化器吸收PM2.5的速度始终不变,则第6小时之后,预计经过多长时间室内PM2.5浓度可恢复正常? -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系xOy中,平行四边形ABCD四个顶点的坐标分别为A(1,1),B(4,1),C(5,2),D(2,2),直线l:y=kx+b与直线y=﹣2x平行.
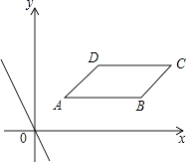

(1)若直线l过点D,求直线l的解析式;
(2)若直线l同时与边AB和CD都相交,求b的取值范围;
(3)若直线l沿线段AC从点A平移至点C,设直线l与x轴的交点为P,问是否存在一点P,使△PAB为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】若一个正数的两个不同的平方根为2与m + 3,则m为___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)﹣150+5﹣(﹣63)
(2)﹣6×(﹣16)﹣(﹣16)÷8.
相关试题

