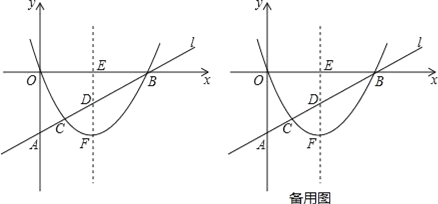
【题目】如图,已知:在平面直角坐标系中,直线l与y轴相交于点A(0,m)其中m<0,与x轴相交于点B(4,0).抛物线y=ax2+bx(a>0)的顶点为F,它与直线l相交于点C,其对称轴分别与直线l和x轴相交于点D和点E.
(1)设a=![]() ,m=﹣2时,
,m=﹣2时,
①求出点C、点D的坐标;
②抛物线y=ax2+bx上是否存在点G,使得以G、C、D、F四点为顶点的四边形为平行四边形?如果存在,求出点G的坐标;如果不存在,请说明理由.
(2)当以F、C、D为顶点的三角形与△BED相似且满足三角形FAC的面积与三角形FBC面积之比为1:3时,求抛物线的函数表达式.
参考答案:
【答案】(1)①(2,﹣1)②(3,﹣ ![]() )(2)y=x2﹣4x
)(2)y=x2﹣4x
【解析】试题分析:(1)①根据待定系数法,可得抛物线的解析式,根据配方法,可得顶点坐标;根据解方程组,可得C点坐标,根据自变量与函数值的对应关系,可得D点坐标;
②根据菱形的性质,可得G点坐标,根据平行四边形的判定,可得答案;
(2)根据待定系数法,可得b与a的关系,根据配方法,可得顶点坐标,根据平行线分线段成比例,可得OH的长,根据自变量与函数值的对应关系,可得C点坐标,根据相似三角形的对应角相等,可得∠FCD=90°,根据相思三角形的性质,可得关于a的方程,根据抛物线的开口向上,可得a的值.
试题解析:(1)①如图1,
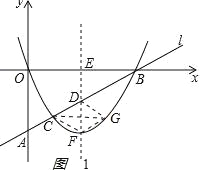 ,
,
当a=![]() 时,将B点坐标代入,得y=
时,将B点坐标代入,得y=![]() x2﹣2x=
x2﹣2x=![]() (x﹣2)2﹣2顶点坐标为(2,﹣2);
(x﹣2)2﹣2顶点坐标为(2,﹣2);
当m=﹣2时,一次函数的解析式为y=![]() x﹣2.
x﹣2.
联立抛物线与直线,得
![]() 2﹣2x=
2﹣2x=![]() x﹣2,
x﹣2,
解得x=1,当x=1时,y=﹣![]() ,即C点坐标为(1,﹣
,即C点坐标为(1,﹣![]() ).
).
当x=2时,y=﹣1,即D点坐标为(2,﹣1);
②假设存在G点,使得以G、C、D、F四点为顶点的四边形是平行四边形.
则CG与DF互相平分,而EF是抛物线的对称轴,且点G在抛物线上
∴CG⊥DF,
∴DCFG是菱形,
∴点C关于EF的对称点G(3,﹣ ![]() ).
).
设DF与CG与DF相交于O′点,则DO′=O′F=![]() ,CO′=O′G=1,
,CO′=O′G=1,
∴四边形DCFG是平行四边形.
∴抛物线y=ax2+bx上存在点G,使得以G、C、D、F四点为顶点的四边形为平行四边形,点G的坐标为(3,﹣ ![]() );
);
(2)如图2,
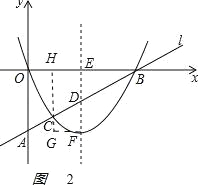 ,
,
∵抛物线y=ax2+bx的图象过(4,0)点,16a+4b=0,
∴b=﹣4a.
∴y=ax2+bx=ax2﹣4ax=a(x﹣2)2﹣4a的对称轴是x=2,
∴F点坐标为(2,﹣4a).
∵三角形FAC的面积与三角形FBC面积之比为1:3,
BC:AC=3:1.
过点C作CH⊥OB于H,过点F作FG∥OB,FG与HC交于G点.
则四边形FGHE是矩形.
由HC∥OA,得BC:AC=3:1.
由HB:OH=3:1,OB=4,OE=EB,得
HE=1,HB=3.
将C点横坐标代入y=ax2﹣4ax,得y=﹣3a.
∴C(1,﹣3a),∴HC=3a,又F(2,﹣4a).
∴GH=4a,GC=a.
在△BED中,∠BED=90°,若△FCD与△BED相似,则△FCD是直角三角形
∵∠FDC=∠BDE<90°,∠CFD<90°,
∴∠FCD=90°.
∴△BHC∽△CGF,
∴![]() ,
,
∴![]() ,
,
∴a2=1,
∴a=±1.
∵a>0,
∴a=1.
∴抛物线的解析式为y=x2﹣4x.
-
科目: 来源: 题型:
查看答案和解析>>【题目】9的平方根等于______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,锐角△ABC的两条高BD、CE相交于点O,且OB=OC.试说明△ABC是等腰三角形.
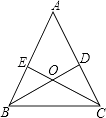
-
科目: 来源: 题型:
查看答案和解析>>【题目】有3张扑克牌,分别是红桃3、红桃4和黑桃5.把牌洗匀后甲先抽取一张,记下花色和数字后将牌放回,洗匀后乙再抽取一张.
(1)列表或画树状图表示所有取牌的可能性;
(2)甲、乙两人做游戏,现有两种方案:A方案:若两次抽得相同花色则甲胜,否则乙胜;B方案:若两次抽得数字和为奇数则甲胜,否则乙胜.请问甲选择哪种方案获胜概率更高?
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道对于x轴上的任意两点A(x1,0),B(x2,0),有AB=|x1﹣x2|,而对于平面直角坐标系中的任意两点P1(x1,y1),P2(x2,y2),我们把|x1﹣x2|+|y1﹣y2|称为Pl,P2两点间的直角距离,记作d(P1,P2),即d(P1,P2)=|x1﹣x2|+|y1﹣y2|.
(1)已知O为坐标原点,若点P坐标为(1,3),则d(O,P)= ;
(2)已知O为坐标原点,动点P(x,y)满足d(O,P)=2,请写出x与y之间满足的关系式,并在所给的直角坐标系中画出所有符合条件的点P所组成的图形;
(3)试求点M(2,3)到直线y=x+2的最小直角距离.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若∠α=24°35′,则∠a的补角的度数为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠B=90°,AB∥CD,M为BC边上的一点,且AM平分∠BAD,DM平分∠ADC.求证:

(1)AM⊥DM;
(2)M为BC的中点.
相关试题

