【题目】我们知道对于x轴上的任意两点A(x1,0),B(x2,0),有AB=|x1﹣x2|,而对于平面直角坐标系中的任意两点P1(x1,y1),P2(x2,y2),我们把|x1﹣x2|+|y1﹣y2|称为Pl,P2两点间的直角距离,记作d(P1,P2),即d(P1,P2)=|x1﹣x2|+|y1﹣y2|.
(1)已知O为坐标原点,若点P坐标为(1,3),则d(O,P)= ;
(2)已知O为坐标原点,动点P(x,y)满足d(O,P)=2,请写出x与y之间满足的关系式,并在所给的直角坐标系中画出所有符合条件的点P所组成的图形;
(3)试求点M(2,3)到直线y=x+2的最小直角距离.

参考答案:
【答案】(1)4;(2)图形见解析;(3)点M(2,3)到直线y=x+2的直角距离为1.
【解析】试题分析:(1)由P0与原点O的坐标,利用题中的新定义计算即可得到结果;
(2)利用题中的新定义列出x与y的关系式,画出相应的图象即可;
(3)根据新的运算规则知d(M,Q)=|x﹣2|+|y﹣3|=|x﹣2|+|x+2﹣3|=|x﹣2|+|x﹣1|,然后由绝对值与数轴的关系可知,|x﹣2|+|x﹣1|表示数轴上实数x所对应的点到数2和1所对应的点的距离之和,其最小值为1.
试题解析:(1)d(O,P)=|0﹣1|+|0﹣3|=4;故答案为:4;
(2)∵O为坐标原点,动点P(x,y)满足d(O,P),
∴|0﹣x|+|0﹣y|=|x|+|y|=2,
所有符合条件的点P组成的图形如图所示;
(3)∵d=|x﹣2|+|y﹣3|=|x﹣2|+|x+2﹣3|=|x﹣2|+|x﹣1|
∴x可取一切实数,|x﹣2|+|x﹣1|表示数轴上实数x所对应的点到1和2所对应的点的距离之和,其最小值为1.
∴点M(2,3)到直线y=x+2的直角距离为1.

-
科目: 来源: 题型:
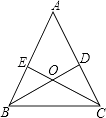
查看答案和解析>>【题目】已知:如图,锐角△ABC的两条高BD、CE相交于点O,且OB=OC.试说明△ABC是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有3张扑克牌,分别是红桃3、红桃4和黑桃5.把牌洗匀后甲先抽取一张,记下花色和数字后将牌放回,洗匀后乙再抽取一张.
(1)列表或画树状图表示所有取牌的可能性;
(2)甲、乙两人做游戏,现有两种方案:A方案:若两次抽得相同花色则甲胜,否则乙胜;B方案:若两次抽得数字和为奇数则甲胜,否则乙胜.请问甲选择哪种方案获胜概率更高?
-
科目: 来源: 题型:
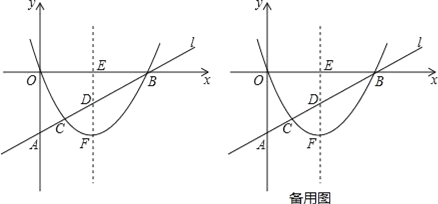
查看答案和解析>>【题目】如图,已知:在平面直角坐标系中,直线l与y轴相交于点A(0,m)其中m<0,与x轴相交于点B(4,0).抛物线y=ax2+bx(a>0)的顶点为F,它与直线l相交于点C,其对称轴分别与直线l和x轴相交于点D和点E.
(1)设a=
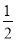 ,m=﹣2时,
,m=﹣2时,①求出点C、点D的坐标;
②抛物线y=ax2+bx上是否存在点G,使得以G、C、D、F四点为顶点的四边形为平行四边形?如果存在,求出点G的坐标;如果不存在,请说明理由.
(2)当以F、C、D为顶点的三角形与△BED相似且满足三角形FAC的面积与三角形FBC面积之比为1:3时,求抛物线的函数表达式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若∠α=24°35′,则∠a的补角的度数为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠B=90°,AB∥CD,M为BC边上的一点,且AM平分∠BAD,DM平分∠ADC.求证:

(1)AM⊥DM;
(2)M为BC的中点. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是△ABC的高,E为AC上一点,BE交AD于H,且有BH=AC,HD=CD.
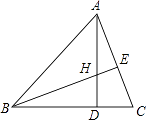
求证:
(1)△BHD≌△ACD;
(2)BE⊥AC.
相关试题

