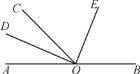
【题目】如图,已知O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.
(1)求∠BOD的度数;(2)OE是否平分∠BOC?说明你的理由.
参考答案:
【答案】(1) 155°;(2)见解析.
【解析】
(1)由角平分线的定义可得∠AOD=25°,再根据平角定义即可求得答案;
(2)分别求出∠COE,∠BOE的值,再做判断即可.
(1)∵∠AOC=50°,OD平分∠AOC,
∴∠AOD=∠COD=![]() ∠AOC=
∠AOC=![]() ×50°=25°,
×50°=25°,
∴∠BOD=180°-∠AOD=155°;
(2)∵∠COD=25°,∠DOE=90°,
∴∠COE=∠DOE-∠DOC=90°-25°=65°,
∵∠BOC=180°-∠AOC=180°-50°=130°,
∴∠BOE=∠BOC-∠EOC=130°-65°=65°,
∴∠BOE =∠COE,
即OE平分∠BOC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两个直角∠AOB,∠COD有相同的顶点O,下列结论:①∠AOC=∠BOD;
②∠AOC+∠BOD=90°;③若OC平分∠AOB,则OB平分∠COD;④∠AOD的平分线与∠COB的平分线是同一条射线. 其中正确的个数有( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】宜宾是国家级历史文化名城,大观楼是标志性建筑之一(如图①).喜爱数学实践活动的小伟查资料得知:大观楼始建于明代(一说是唐代韦皋所建),后毁于兵火,乾隆乙酉年(1765年)重建,它是我国目前现存最高大、最古老的楼阁之一.小伟决定用自己所学习的知识测量大观楼的高度.如图②,他利用测角仪站在B处测得大观楼最高点P的仰角为45°,又前进了12米到达A处,在A处测得P的仰角为60°.请你帮助小伟算算大观楼的高度.(测角仪高度忽略不计,
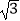 ≈1.7,结果保留整数).
≈1.7,结果保留整数).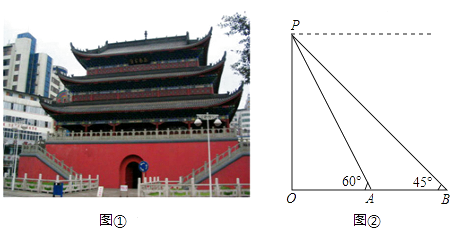
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=x﹣1与反比例函数y=
 的图象交于A、B两点,与x轴交于点C,已知点A的坐标为(﹣1,m).
的图象交于A、B两点,与x轴交于点C,已知点A的坐标为(﹣1,m). 
(1)求反比例函数的解析式;
(2)若点P(n,﹣1)是反比例函数图象上一点,过点P作PE⊥x轴于点E,延长EP交直线AB于点F,求△CEF的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,∠B=∠CAD.

(1)求证:AC是⊙O的切线;
(2)若点E是 的中点,连接AE交BC于点F,当BD=5,CD=4时,求AF的值.
的中点,连接AE交BC于点F,当BD=5,CD=4时,求AF的值. -
科目: 来源: 题型:
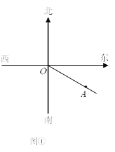
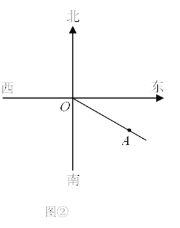
查看答案和解析>>【题目】如图①,货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上,同时,在它北偏东30°、西北(即北偏西45°)方向上又分别发现了客轮B和海岛C.
(1)请分别在图①中画出表示客轮B和海岛C方向的射线OB,OC(不写作法);
(2)若图中有一艘渔船D,且∠AOD的补角是它的余角的3倍,在图②中画出表示渔船D方向的射线OD,并求渔船D在货轮O的方位角.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将从1开始的连续自然数按图规律排列:规定位于第3行,第2列的自然数10记为(3,2),自然数15记为(4,2)…….
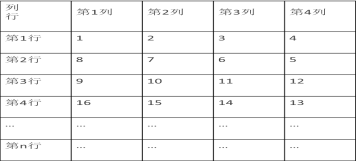
按此规律,回答下列问题:
(1)记为(6,3)表示的自然数是___________;
(2)自然数2018记为 __________;
(3)用一个正方形方框在第3列和第4列中任意框四个数,这四个数的和能为2018吗?如果能,求出框出的四个数中最小的数;如果不能,请写出理由.
相关试题

