【题目】如图,为了测量合浦文昌塔的高度,某校兴趣小组在塔前的平地A处安装了测角仪,测得塔顶的仰角∠α=30°,又沿着塔的方向前进25米到达B处测量,测得塔顶的仰角∠β=45°,已知测角仪的高AC=1.5米,请你根据上述数据,计算塔FG的高度(结果精确到0.1米).
参考答案:
【答案】解:设EF=x米,
在Rt△FDE中,
∵∠FDE=∠DFE=45°,
∴DE=EF=x米,
∴CE=(x+25)米,
Rt△CEF中,
∵∠FCE=30°,
∴ ![]() =tan∠C=
=tan∠C= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得:x= ![]() (
( ![]() +1)米,
+1)米,
∴FG=EF+EG=EF+AC= ![]() (
( ![]() +1)+1.5≈35.7(米).
+1)+1.5≈35.7(米).
答:古塔的高约为35.7米.
【解析】设EF=x米,在Rt△FDE中,∠FDE=∠DFE=45°,可得出DE=EF,CE=x+25,在Rt△CEF中利用锐角三角函数的定义即可求出x的值,进而可得出结论.
【考点精析】认真审题,首先需要了解锐角三角函数的定义(锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数).
-
科目: 来源: 题型:
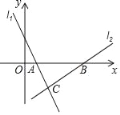
查看答案和解析>>【题目】如图,直线l1的函数表达式为y=﹣2x+2,且与x轴交于点A,直线l2经过点B(5,0)且与l1交于点C,已知点C的横坐标是2.
(1)求点A和点C的坐标;
(2)若在直线l2上存在异于点C的另一点M,使得△ABM与△ABC的面积相等,试求点M的坐标.
(3)在y轴上求点P的坐标,使得PA+PC最小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,O为对角线AC的中点,EF经过点O并与AB,CD分别相交于点E,F.
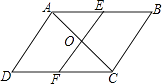
(1)求证:AE=CF;
(2)当EF⊥AC时,连接AF,CE,试判断四边形AFCE是怎样的四边形?并证明你的结论. -
科目: 来源: 题型:
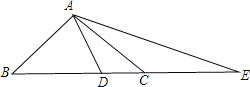
查看答案和解析>>【题目】(1)如图,在在△ABC中,已知∠BAC=900,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上,CE=CA,求∠DAE的度数;
(2)如果把(1)中的“AB=AC”条件去掉,其余条件不变,那么∠DAE的度数改变吗?为什么?
(3)如果把(1)中的“∠BAC=900”改成“∠BAC>900”其余条件不变,试探究∠DAE与∠BAC的数量关系式,试证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形ABCD中,AB=2,BC=1,运点P从点B出发,沿路线B
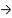 C
C D作匀速运动,那么△ABP的面积
D作匀速运动,那么△ABP的面积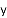 与点P运动的路程之间的函数图象大致是( ).
与点P运动的路程之间的函数图象大致是( ).
A.
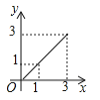 B.
B. 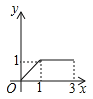 C.
C. 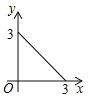 D.
D. 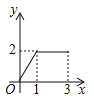
-
科目: 来源: 题型:
查看答案和解析>>【题目】数轴上有A、B两点,A在B的左侧,已知点B对应的数为2,点A对应的数为a.
(1)若a=﹣3,则线段AB的长为 (直接写出结果);
(2)若点C在线段AB之间,且AC﹣BC=2,求点C表示的数(用含a的式子表示);
(3)在(2)的条件下,点D是数轴上A点左侧一点,当AC=2AD,BD=4BC,求a的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:已知两直线,L1:y=k1x+b1,L2:y=k2x+b2,
若L1⊥L2,则有k1k2=﹣1,根据以上结论解答下列各题:
(1)已知直线y=2x+1与直线y=kx﹣1垂直,求k的值;
(2)若一条直线经过A(2,3),且与y=﹣
 x+3垂直,求这条直线所对应的一次函数的关系式.
x+3垂直,求这条直线所对应的一次函数的关系式.
相关试题

