【题目】阅读理解:已知两直线,L1:y=k1x+b1,L2:y=k2x+b2,
若L1⊥L2,则有k1k2=﹣1,根据以上结论解答下列各题:
(1)已知直线y=2x+1与直线y=kx﹣1垂直,求k的值;
(2)若一条直线经过A(2,3),且与y=﹣![]() x+3垂直,求这条直线所对应的一次函数的关系式.
x+3垂直,求这条直线所对应的一次函数的关系式.
参考答案:
【答案】(1)-![]() ;(2)y=3x﹣3
;(2)y=3x﹣3
【解析】
(1)根据两直线互相垂直,两个函数的比例系数k的乘积是﹣1列方程求解即可;
(2)根据y=﹣![]() x+3设出直线l1的解析式,然后将点A的坐标代入计算,从而得解.
x+3设出直线l1的解析式,然后将点A的坐标代入计算,从而得解.
(1)∵L1⊥L2,则有k1k2=﹣1,
∴2k=﹣1,
∴k=﹣![]() ;
;
(2)∵过点A的直线与y=﹣![]() x+3垂直,
x+3垂直,
∴设过点A的直线解析式为y=3x+b,
将点A(2,3)代入,得:6+b=3,
解得:b=﹣3,
所以过点A的直线解析式为y=3x﹣3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为了测量合浦文昌塔的高度,某校兴趣小组在塔前的平地A处安装了测角仪,测得塔顶的仰角∠α=30°,又沿着塔的方向前进25米到达B处测量,测得塔顶的仰角∠β=45°,已知测角仪的高AC=1.5米,请你根据上述数据,计算塔FG的高度(结果精确到0.1米).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形ABCD中,AB=2,BC=1,运点P从点B出发,沿路线B
 C
C D作匀速运动,那么△ABP的面积
D作匀速运动,那么△ABP的面积 与点P运动的路程之间的函数图象大致是( ).
与点P运动的路程之间的函数图象大致是( ).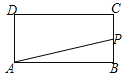
A.
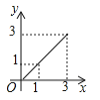 B.
B. 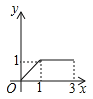 C.
C. 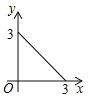 D.
D. 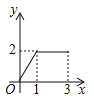
-
科目: 来源: 题型:
查看答案和解析>>【题目】数轴上有A、B两点,A在B的左侧,已知点B对应的数为2,点A对应的数为a.
(1)若a=﹣3,则线段AB的长为 (直接写出结果);
(2)若点C在线段AB之间,且AC﹣BC=2,求点C表示的数(用含a的式子表示);
(3)在(2)的条件下,点D是数轴上A点左侧一点,当AC=2AD,BD=4BC,求a的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上,同时,在它北偏东30°、西北(即北偏西45°)方向上又分别发现了客轮B和海岛C.
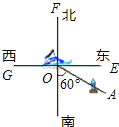
(1)仿照表示灯塔方位的方法,分别画出表示客轮B和海岛C方向的射线OB,OC(不写作法);
(2)若图中有一艘渔船D,且∠AOD的补角是它的余角的3倍,画出表示渔船D方向的射线OD,则渔船D在货轮O的 (写出方位角)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校的复印任务原来由甲复印社承接,其收费y(元)与复印页数x(页)的关系如下表:
x(页)
100
200
400
1000
…
y(元)
40
80
160
400
(1)若y与x满足初中学过的某一函数关系,求函数的解析式;
(2)现在乙复印社表示:若学校先按每月付给200元的承包费,则可按每页0.15元收费.则乙复印社每月收费y(元)与复印页数x(页)的函数关系为 ;
(3)应选择哪个复印社比较优惠?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABP是等腰三角形,AB=BP,以AB为直径的⊙O交AP于点D,交BP于点C,连接BD交AC于点G,直线MN过点A,且∠PAM=
 ∠ABP.
∠ABP.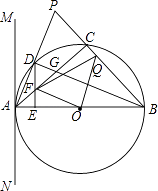
(1)试说明直线MN是⊙O的切线.
(2)过D作DE⊥AB于E,交AC于F,求证:△DFG是等腰三角形.
(3)连结FO,过点O作OQ⊥FO交BP于点Q,连结FQ,求证:FQ2=AF2+BQ2 .
相关试题

