【题目】在平面直角坐标系中,A(-2,0),C(2,2),过C作CB⊥x轴于B.
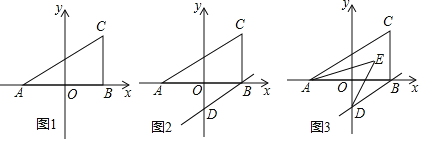
(1)如图1,△ABC的面积是 ;
(2)如图1,在y轴上找一点P,使得△ABP的面积与△ABC的面积相等,请直接写出P点坐标: ;
(3)如图2,若过B作BD∥AC交y轴于D,则∠BAC+∠ODB的度数为 度;
(4)如图3,BD∥AC,若AE、DE分别平分∠CAB,∠ODB,求∠AED的度数.
参考答案:
【答案】(1)4;(2)(0,2)或(0,-2);(3)90;(4)45°.
【解析】
(1)根据题意求出OB的长,根据三角形的面积公式计算即可;
(2)设P点坐标为(0,y),根据三角形的面积公式列出方程,解方程即可;
(3)根据平行线的性质、直角三角形的两锐角互余解答;
(4)连接AD,根据角平分线的定义得到AE,DE分别平分∠CAB,∠ODB,得到∠EAO+∠EDO=45°,根据三角形内角和定理计算即可.
(1)∵点C的坐标为(2,2),CB⊥x轴于B,
∴点B的坐标为(2,0),即OB=2,
∴AB=2+2=4,
则△ABC的面积=![]() ×4×2=4,
×4×2=4,
故答案为:4;
(2)设P点坐标为(0,y),
由题意得,![]() ×4×|y|=4,
×4×|y|=4,
解得,y=±2,
则P点坐标为(0,2)或(0,-2),
故答案为:(0,2)或(0,-2);
(3)∵BD∥AC,
∴∠BAC=∠ABD,
∵∠OBD+∠ODB=90°,
∴∠BAC+∠ODB=90°,
故答案为:90;
(4)连接AD,
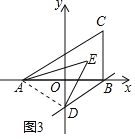
∵AE,DE分别平分∠CAB,∠ODB,
∴∠EAO=![]() ∠BAC,∠EDO=
∠BAC,∠EDO=![]() ∠ODB,
∠ODB,
∴∠EAO+∠EDO=![]() (∠BAC+∠ODB)=45°,
(∠BAC+∠ODB)=45°,
∵∠AED+∠EAD+∠EDA=180°,即∠AED+∠EAO+∠OAD+∠EDO+∠ODA=180°,
∵∠OAD+∠ODA=90°,
∴∠AED+45°+90°=180°,
∴∠AED=45°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O的另一个交点为E,连接AC,CE.
(1)求证:∠B=∠D;
(2)若AB=4,BC﹣AC=2,求CE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点A(-2,2),B(0,5),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,得到△A1B1C,请画出△A1B1C的图形.
(2)平移△ABC,使点A的对应点A2坐标为(-2,-6),请画出平移后对应的△A2B2C2的图形.
(3)若将△A1B1C绕某一点旋转可得到△A2B2C2,请直接写出旋转中心的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】定义一种新运算“a*b”:当a≥b时,a*b=a+2b;当a<b时,a*b=a-2b.
例如:3*(-4)=3+(-8)=-5,(-6)*12=-6-24=-30
(1)填空:(-4)*3= .
(2)若(3x-4)*(x+6)=(3x-4)+2(x+6),则x的取值范围为 ;
(3)已知(3x-7)*(3-2x)<-6,求x的取值范围;
(4)小明在计算(2x2-4x+8)*(x2+2x-2)时随意取了一个x的值进行计算,得出结果是-4,小丽告诉小明计算错了,问小丽是如何判断的.
-
科目: 来源: 题型:
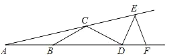
查看答案和解析>>【题目】如图,若A 15, AB BC CD DE EF ,则DEF 等于________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,线段AB经过圆心O,交⊙O于A、C两点,点D在⊙O上,∠A=∠B=30°.
(1)求证:BD是⊙O的切线;
(2)若点N在⊙O上,且DN⊥AB,垂足为M,NC=10,求AD的长.
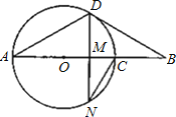
-
科目: 来源: 题型:
查看答案和解析>>【题目】在ABC 中, AB AC , BAC=100°,点 D 在 BC 上, ABD 和AFD 关于直线 AD 对称, FAC 的平分线交 BC 于点 G,连接 FG 当BAD _________.时,DFG为等腰三角形.
相关试题

