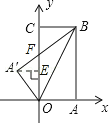
【题目】如图,把一个矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴、y轴上,连接OB,将纸片OABC沿OB折叠,使点A落在A′的位置上.若OB=![]() ,
,![]() ,求点A′的坐标为 .
,求点A′的坐标为 . 
参考答案:
【答案】(![]() ,
,![]() )
)
【解析】∵OB= ![]() ,
, ![]()
∴BC=1,OC=2
设OC与A′B交于点F,作A′E⊥OC于点E
∵纸片OABC沿OB折叠
∴OA=OA′,∠BAO=∠BA′O=90°
∵BC∥A′E
∴∠CBF=∠FA′E
∵∠AOE=∠FA′O
∴∠AOE=∠CBF
∴△BCF≌△OA′F
∴OA′=BC=1,设A′F=x
∴OF=2﹣x
∴A′F=![]() ,OF=
,OF=![]()
∵A′E=A′F×OA′÷OF= ![]()
∴OE=![]()
∴点A’的坐标为(![]() ,
,![]() ).
).
所以答案是:(![]() ,
,![]() ).
).
【考点精析】关于本题考查的矩形的性质和翻折变换(折叠问题),需要了解矩形的四个角都是直角,矩形的对角线相等;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能得出正确答案.
-
科目: 来源: 题型:
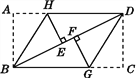
查看答案和解析>>【题目】如图,把一张长方形纸片ABCD按图中的方式折叠,使点A与点E重合,点C与点F重合(E,F两点均在BD上),折痕分别为BH,DG.试说明:△BHE≌△DGF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明袋子中有1个红球,1个绿球和n个白球,这些球除颜色外无其他差别.
(1)当n=1时,从袋中随机摸出1个球,摸到红球和摸到白球的可能性是否相同?
(2)从袋中随机摸出一个球,记录其颜色,然后放回.大量重复该试验,发现摸到绿球的频率稳定于0.25,求n的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察如图等式:在数字宝塔中,从上往下数,2017在第层.
第一层1+2=3
第二层4+5+6=7+8
第三层9+10+11+12=13+14+15
第四层16+17+18+19+20=21+22+23+24 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,那么阴影部分的面积是矩形ABCD的面积是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x2+y2=10,xy=3,则x+y=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一条弯曲的公路改为直道,可以缩短路程,其道理用几何知识解释的应是( )
A.两点之间线段最短B.两点确定一条直线
C.线段可以大小比较D.线段有两个端点
相关试题

