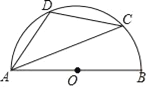
【题目】如图,AB是半圆的直径,C、D是半圆上的两点,且∠BAC=20°,![]() .请连结线段CB,求四边形ABCD各内角的度数.
.请连结线段CB,求四边形ABCD各内角的度数.

参考答案:
【答案】55°,70°,125°,110°
【解析】试题分析:连结BC,根据圆周角定理得∠ACB=90°,则利用互余可计算出∠B=70°,再根据圆内接四边形的性质计算出∠D=180°﹣∠B=110°,接着根据圆周角定理和三角形内角和定理,由弧AD=弧CD得到∠DAC=∠DCA=35°,然后计算∠DAB=∠DAC+∠BAC=55°,∠DCB=∠DCA+∠ACB=125°.
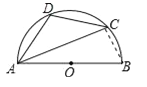
试题解析:解:连结BC,如图,∵AB是半圆的直径,∴∠ACB=90°,∵∠BAC=20°,∴∠B=70°,∵四边形ABCD是圆O的内接四边形,∴∠D=180°﹣∠B=110°,∵弧AD=弧CD,∴∠DAC=∠DCA=![]() (180°-110°)=35°,∴∠DAB=∠DAC+∠BAC=55°,∠DCB=∠DCA+∠ACB=125°,即四边形ABCD各内角的度数分别为55°,70°,125°,110°.
(180°-110°)=35°,∴∠DAB=∠DAC+∠BAC=55°,∠DCB=∠DCA+∠ACB=125°,即四边形ABCD各内角的度数分别为55°,70°,125°,110°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC绕点A顺时针旋转60°得到△ADE,点C的对应点E恰好落在BA的延长线上,DE与BC交于点F,连接BD.下列结论不一定正确的是( )

A. AD=BD B. AC∥BD C. DF=EF D. ∠CBD=∠E
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,经过点B(﹣2,0)的直线y=kx+b与直线y=4x+2相交于点A(﹣1,﹣2),4x+2<kx+b<0的解集为( )
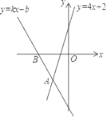
A.x<﹣2B.﹣2<x<﹣1C.x<﹣1D.x>﹣1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是正
是正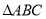 内一点,
内一点,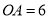 ,
,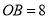 ,
,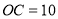 ,将线段
,将线段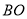 以点
以点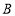 为旋转中心逆时针旋转60°得到线段
为旋转中心逆时针旋转60°得到线段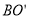 ,下列结论:①
,下列结论:①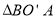 可以由
可以由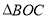 绕点
绕点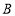 逆时针旋转60°得到;②点
逆时针旋转60°得到;②点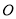 与
与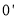 的距离为6;③
的距离为6;③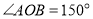 ;④
;④ ;⑤
;⑤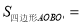
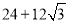 .其中正确的结论是(填序号)______.
.其中正确的结论是(填序号)______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为保护环境,我市公交公司计划购买A型和B型两种环保节能公交车共10辆.若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元.
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在某线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于680万人次,则该公司有哪几种购车方案?
(3)在(2)的条件下,哪种购车方案总费用最少?最少总费用是多少万元?
-
科目: 来源: 题型:
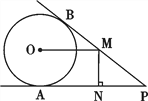
查看答案和解析>>【题目】如图,PA,PB分别与⊙O相切于点A,B,点M在PB上,且OM∥AP,MN⊥AP,垂足为N.
(1)求证:OM = AN;
(2)若⊙O的半径R = 3,PA = 9,求OM的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, ,且
,且 面积是24,
面积是24, 的垂直平分线
的垂直平分线 分别交
分别交 边于点
边于点 ,若点
,若点 为
为 边的中点,点
边的中点,点 为线段
为线段 上一动点,则
上一动点,则 周长的最小值为( )
周长的最小值为( )
A.9B.10C.11D.12
相关试题

