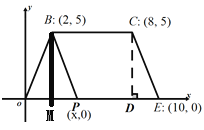
【题目】如图，在平面直角坐标系内，四边形OECB的顶点坐标分别是：B（2，5），C（8，5），E（10，0），点P（x，0）是线段OE上一点，设四边形BPEC的面积为S．

（1）过点C作CD⊥x轴于点E，则CD= ， 用含x的代数式表示PE= .

（2）求S与x的函数关系．

（3）当S＝30时，直接写出线段PE与PB的长．

参考答案：

【答案】（1）CD=5，PE=10-x；（2）（3）PE=6，PB=

【解析】试题分析：（1）根据点D的坐标直接求得CD的长，根据点E的坐标表示出PE的长即可；（2）根据已知条件可知四边形BPEC是梯形，利用梯形的面积公式即可求解.(2)把S=30 代入求得x的值，即可求得PE的长，过点B作BM⊥X轴于点M，在Rt△BPM中，根据勾股定理求得PB的长即可.

试题解析：

（1）CD=5，PE=10-x；

（2）∵B（2，5），C（8，5），

∴BC=6，BC∥x轴，

∴S= .

(3)把S=30 代入得，x=4，

∴PE=6.

如图，过点B作BM⊥X轴于点M，

∵B（2，5），OP=4，

∴BM=5，PM=2，

在Rt△BPM中，根据勾股定理求得PB=.

关闭