搜索
【题目】如图，直钱AB、CD相交于点O，OD平分∠AOF，OE⊥CD于O．∠EOA=50°．求∠BOC、∠BOE、∠BOF的度数．
参考答案：
【答案】40°； 130° ； 100°.
【解析】
由垂直的定义可求∠AOD=40，根据对顶角相等求出∠BOC=40，由∠BOE=∠EOC＋∠BOC可求出∠BOE的度数，由角平分线的定义可求出∠DOF=∠AOD=40°，根据∠BOF=∠COD-∠BOC-∠DOF可求出∠BOF的度数.
解：∵OE⊥CD于O
∴∠EOD=∠EOC=90°
∵∠AOD=∠EOD-∠AOE,∠EOA=50°
∴∠AOD=90－50=40
∴∠BOC=∠AOD=40
∵∠BOE=∠EOC＋∠BOC
∴∠BOE=90°＋40°=130°
∵OD平分∠AOF
∴∠DOF=∠AOD=40°
∴∠BOF=∠COD-∠BOC-∠DOF=180°-40°-40°=100°
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知AB是⊙O的直径，点P在BA的延长线上，PD切⊙O于点D，过点B作BE垂直于PD，交PD的延长线于点C，连接AD并延长，交BE于点E．
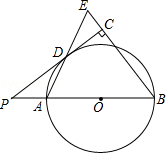
（1）求证：AB=BE；
（2）若PA=2，cosB=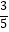
，求⊙O半径的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图有四条互相不平行的直线l1、l2、l3、l4所截出的七个角，关于这七个角的度数关系，下列结论正确的是（ ）
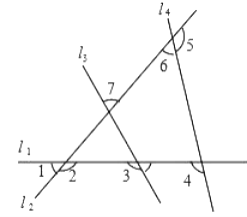
A. ∠2=∠4+∠7 B. ∠3=∠1+∠7
C. ∠1+∠4+∠6=180° D. ∠2+∠3+∠5=360°
-
科目： 来源： 题型：
查看答案和解析>>【题目】一次函数y=kx﹣1的图象经过点P，且y的值随x值的增大而增大，则点P的坐标可以为（ ）
A. （﹣5，3） B. （1，﹣3） C. （2，2） D. （5，﹣1）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知直线EF与AB交于点M，与CD交于点O，OG平分∠DOF，若∠COM=120°，∠EMB=
∠COF． 
（1）求∠FOG的度数；
（2）写出一个与∠FOG互为同位角的角；
（3）求∠AMO的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知如图，在长方形ABCD中，点E是AD的中点，连结BE，将△ABE沿着BE翻折得到△FBE，EF交BC于点H，延长BF、DC相交于点G，若DG=16，BC=24，则AB=________．
-
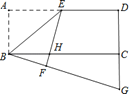
科目： 来源： 题型：
查看答案和解析>>【题目】已知一次函数y1＝kx＋b的图像经过点（0，-2），（2，2）.
（1）求一次函数的表达式，并在所给直角坐标系中画出此函数的图像；；
（2）根据图像回答：当x 时，y1=0；
（3）求直线y1＝kx＋b、直线y2＝-2x+4与y轴围成的三角形的面积．
相关试题
