【题目】用配方法解下列方程:
(1)4x2 -4x -1 = 0; (2)7x2 -28x +7= 0.
(3) ![]() x2-x-4=0 (4) 3x2-45=30x
x2-x-4=0 (4) 3x2-45=30x
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]()
【解析】试题分析:(1)把二次项系数化为1,常数项移到等号右边,两边都加上一次项系数一半的平方,配成完全平方式,然后开平方即可得出答案;
(2)把二次项系数化为1,常数项移到等号右边,两边都加上一次项系数一半的平方,配成完全平方式,然后开平方即可得出答案;
(3)把二次项系数化为1,常数项移到等号右边,两边都加上一次项系数一半的平方,配成完全平方式,然后开平方即可得出答案;
(4)整理成一般式,把二次项系数化为1,常数项移到等号的右边后,两边都加上一次项系数一半的平方,配成完全平方式,然后开平方即可得出答案.
试题解析:(1)4x2 -4x -1 = 0,
x2-x-![]() =0,
=0,
x2-x=![]() ,
,
x2-x+![]() =
=![]() +
+![]() ,即(x-
,即(x-![]() )2=
)2=![]() ,
,
则x-1=±![]() ,
,
![]() ;
;
(2)7x2 -28x +7= 0,
x2-4x=-1,
x2-4x+22=-1+22,即(x-2)2=3,
则x-2=±![]() ,
,
x=2±![]() ,
,
即![]() ;
;
(3)![]() x2-x-4=0
x2-x-4=0
x2-4x=16,
x2-4x+22=16+22,即(x-2)2=20,
则x-2=±![]() ,
,
x=2±![]() ,
,
即![]() ;
;
(4)3x2-45=30x,
x2-10x=15,
x2-10x+52=15+52,即(x-5)2=40,
则x-5=±![]() ,
,
x=5±![]() ,
,
即![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,现将一块等腰直角三角板ABC放在第二象限,斜靠在两坐上,且点A(0,2),点C(
 ,0),如图所示:抛物线
,0),如图所示:抛物线 经过点B。
经过点B。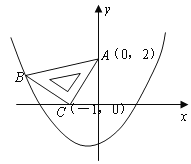
(1)求点B的坐标;
(2)求抛物线的解析式;
(3)在抛物线上是否还存在点P(点B除外),使△ACP仍然是以AC为直角边的等腰直角三角形?若存在,求所有点P的坐标;若不存在,请说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】将下列各式配成完全平方式:
①x2+6x+______=(x+____)2 ②x2-5x+_____=(x-____)2;
③x2+ x+______=(x+____)2 ④x2-9x+_____=(x-____)2
-
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法解下列方程:
(1)x2+2x-8=0 (2)x2+12x-15=0
(3)x2-4x=16 (4)x2=x+56
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图
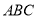 中任一点
中任一点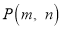 经过平移后对应点为
经过平移后对应点为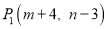 .将
.将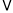
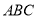 作同样的平移得到
作同样的平移得到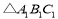 ,已知
,已知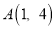 ,
,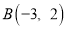 ,
,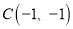 ,
,(1) 在图中画出
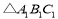 ,;
,;(2) 直接写出
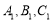 的坐标分别为
的坐标分别为
(3)
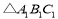 ,的面积为____________.
,的面积为____________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图四边形ABCD是菱形,且∠ABC=60,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM,则下列五个结论中正确的是( )
①若菱形ABCD的边长为1,则AM+CM的最小值1;
②△AMB≌△ENB;
③S四边形AMBE=S四边形ADCM;
④连接AN,则AN⊥BE;
⑤当AM+BM+CM的最小值为2
 时,菱形ABCD的边长为2.
时,菱形ABCD的边长为2.
A. ①②③ B. ②④⑤ C. ①②⑤ D. ②③⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于实数a,我们规定:用符号
 表示不大于
表示不大于 的最大整数,称
的最大整数,称 为a的根整数,例如:
为a的根整数,例如: ,
, =3.
=3.(1)仿照以上方法计算:
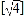 =______;
=______; =_____.
=_____.(2)若
 ,写出满足题意的x的整数值______.
,写出满足题意的x的整数值______.如果我们对a连续求根整数,直到结果为1为止.例如:对10连续求根整数2次


 =1,这时候结果为1.
=1,这时候结果为1.(3)对100连续求根整数,____次之后结果为1.
(4)只需进行3次连续求根整数运算后结果为1的所有正整数中,最大的是____.
相关试题

