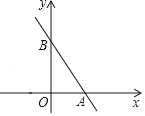
【题目】如图,直线l的解析式为y=﹣![]() x+b,它与坐标轴分别交于A、B两点,其中点B坐标为(0,4).
x+b,它与坐标轴分别交于A、B两点,其中点B坐标为(0,4).
(1)求出A点的坐标;
(2)在第一象限的角平分线上是否存在点Q使得∠QBA=90°?若存在,求点Q的坐标;若不存在,请说明理由.
(3)动点C从y轴上的点(0,10)出发,以每秒1cm的速度向负半轴运动,求出点C运动所有的时间t,使得△ABC为轴对称图形(直接写答案即可)
参考答案:
【答案】(1)A(3,0);(2)存在.Q(16,16);(3)当C点运动1秒、![]() 秒、11秒、14秒时,能使△ABC为轴对称图形.
秒、11秒、14秒时,能使△ABC为轴对称图形.
【解析】
(1)利用点B代入直线,求出直线解析式,然后求直线与x轴交点坐标;
(2)点Q在第一象限角平分线上,设Q(x,x),已知给出了指定角,利用勾股定理列方程,即可求出点Q的标;
(3)求△ABC为轴对称图形,实质是求动点C,使△ABC为等腰三角形,根据等腰三角形性质分类讨论即可求出点的坐标,利用点的坐标求出运动时间.
(1)将点B(0,4)代入直线l的解析式得:
b=4,
∴直线l的解析式为:y=﹣![]() x+4,
x+4,
令y=0得:x=3,
∴A(3,0).
(2)存在.
∵Q在第一象限的角平分线上,
设Q(x,x),
根据勾股定理:
QB2+BA2=QA2,
x2+(x﹣4)2+52=x2+(x﹣3)2,
解得x=16,
故Q(16,16).
(3)能使△ABC为轴对称图形,
则得:△ABC为等腰三角形,
当AB=BC时,
C(0,9)或(0,﹣1),
此时C点运动1秒或11秒,
当AB=AC时,
C(0,﹣4),
此时C点运动14秒,
当AC=BC时,
C(0,![]() ),
),
此时C点运动![]() 秒.
秒.
综上所述:当C点运动1秒、![]() 秒、11秒、14秒时,能使△ABC为轴对称图形.
秒、11秒、14秒时,能使△ABC为轴对称图形.
-
科目: 来源: 题型:
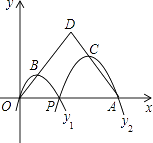
查看答案和解析>>【题目】如图,已知点A(4,0),O为坐标原点,P是线段OA上任意一点(不含端点O,A),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB与AC相交于点D.当OD=AD=3时,这两个二次函数的最大值之和等于( )
A.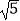
B.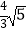
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.阜阳市某家快递公司,2017年3月份与5月份完成投递的快递总件数分别为10万件和12.1万件.现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递快递总件数的月平均增长率?
(2) 如果平均每人每月最多可投递快递0.6万件,那么该公司现有的21名快递投递业务员能否完成2017年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如图所示,如果AF=4,AB=7,

(1)指出旋转中心和旋转角度;
(2)求DE的长度;
(3)BE与DF的位置关系如何?
-
科目: 来源: 题型:
查看答案和解析>>【题目】河南省旅游资源丰富,2013~2017年旅游收入不断增长,同比增速分别为:15.3%,12.7%,15.3%,14.5%,17.1%.关于这组数据,下列说法正确的是( )
A. 中位数是12.7% B. 众数是15.3%
C. 平均数是15.98% D. 方差是0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将正△ABC分割成m个边长为1的小正三角形和一个黑色菱形,这个黑色菱形可分割成n个边长为1的小三角形,若
 =
= 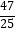 ,则△ABC的边长是 .
,则△ABC的边长是 . 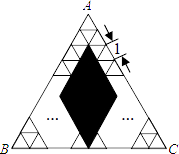
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在ABCD中,点F在AB的延长线上,且BF=AB,连接FD,交BC于点E.
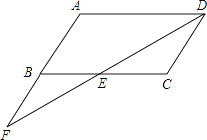
(1)说明△DCE≌△FBE的理由;
(2)若EC=3,求AD的长.
相关试题

