【题目】已知线段OA⊥OB,C为OB上中点,D为AO上一点,连AC、BD交于P点.

(1)如图1,当OA=OB且D为AO中点时,求![]() 的值;
的值;
(2)如图2,当OA=OB,![]() 时,求tan∠BPC.
时,求tan∠BPC.
参考答案:
【答案】(1)2;(2)![]() .
.
【解析】
试题分析:(1)过D作BO的平行线,根据平行线分线段成比例定理,在△ACO中ED:CO=AD:AO,在△ADE和△PCB中,ED:BC=PE:PC,再根据C是BO的中点,可以求出PE:PC=1:2,再根据三角形中位线定理,E是AC的中点,利用比例变形求出AP与PC的比值等于2;
(2)同(1)的方法,先求出PC=![]() AC,再过D作DF⊥AC于F,设AD为a,利用勾股定理求出AC等于2
AC,再过D作DF⊥AC于F,设AD为a,利用勾股定理求出AC等于2 ![]() a,再利用相似三角形对应边成比例求出DF、AF的值,而PF=AC﹣AF﹣PC,也可求出,又∠BPC与∠FPD是对顶角,所以其正切值便可求出.
a,再利用相似三角形对应边成比例求出DF、AF的值,而PF=AC﹣AF﹣PC,也可求出,又∠BPC与∠FPD是对顶角,所以其正切值便可求出.
解:(1)过D作DE∥CO交AC于E,
∵D为OA中点,∴AE=CE=![]() ,
,![]() ,
,
∵点C为OB中点,
∴BC=CO,![]() ,
,
∴![]() ,
,
∴PC=![]() =
=![]() ,
,
∴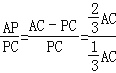 =2;
=2;
(2)过点D作DE∥BO交AC于E,
∵![]() ,∴
,∴![]() =
=![]() =
=![]() ,
,
∵点C为OB中点,∴![]() ,
,
∴![]() ,∴PC=
,∴PC=![]() =
=![]() ,
,
过D作DF⊥AC,垂足为F,设AD=a,则AO=4a,
∵OA=OB,点C为OB中点,∴CO=2a,
在Rt△ACO中,AC=![]() =
=![]() =2
=2 ![]() a,
a,
又∵Rt△ADF∽Rt△ACO,∴![]() ,
,
∴AF=![]() ,DF=
,DF=![]() ,
,
PF=AC﹣AF﹣PC=2 ![]() a﹣
a﹣![]() ﹣
﹣![]() =
=![]() ,
,
tan∠BPC=tan∠FPD=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】体育课上,老师测量跳远成绩的依据是( )
A. 平行线间的距离相等 B. 两点之间,线段最短 C. 垂线段最短 D. 两点确定一条直线
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的方程x2+3x+a=0有一个根为﹣1,则另一个根为( )
A.﹣2 B.2 C.4 D.﹣3
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,属于真命题的是( )
A. 同位角相等
B. 任意三角形的外角一定大于内角
C. 多边形的内角和等于180°
D. 同角或等角的余角相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】轮船从B处以每小时50海里的速度沿南偏东30°方向匀速航行,在B处观测灯塔A位于南偏东75°方向上,轮船航行半小时到达C处,在C处观测灯塔A位于北偏东60°方向上,则C处与灯塔A的距离是( )海里.
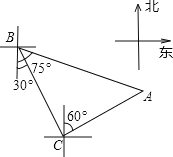
A.25
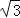 B.25
B.25 C.50 D.25
C.50 D.25 -
科目: 来源: 题型:
查看答案和解析>>【题目】线段CD是由线段AB平移得到的.点A(﹣1,4)的对应点为C(4,7),则点B(﹣4,﹣1)的对应点D的坐标为( )
A. (2,9) B. (5,3) C. (1,2) D. (﹣9,﹣4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在坐标系中,正比例函数y=﹣x的图象与反比例函数y=
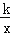 的图象交于A、B两点.
的图象交于A、B两点.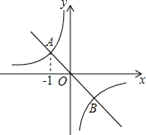
①试根据图象求k的值;
②P为y轴上一点,若以点A、B、P为顶点的三角形是直角三角形,试直接写出满足条件的点P所有可能的坐标.
相关试题

