【题目】在平面直角坐标系![]() 中,规定:抛物线
中,规定:抛物线![]() 的伴随直线为
的伴随直线为![]() .例如:抛物线
.例如:抛物线![]() 的伴随直线为
的伴随直线为![]() ,即
,即![]()
(1)在上面规定下,抛物线![]() 的顶点为 .伴随直线为 ;抛物线
的顶点为 .伴随直线为 ;抛物线![]() 与其伴随直线的交点坐标为 和 ;
与其伴随直线的交点坐标为 和 ;
(2)如图,顶点在第一象限的抛物线![]() 与其伴随直线相交于点
与其伴随直线相交于点![]() (点
(点![]() 在点
在点![]() 的右侧)与
的右侧)与![]() 轴交于点
轴交于点![]()
①若![]() 求
求![]() 的值;
的值;
②如果点![]() 是直线
是直线![]() 上方抛物线的一个动点,
上方抛物线的一个动点,![]() 的面积记为
的面积记为![]() ,当
,当![]() 取得最大值
取得最大值![]() 时,求
时,求![]() 的值.
的值.

参考答案:
【答案】(1)(﹣1,﹣4);y=x﹣3;(0,﹣3);(﹣1,﹣4);(2)①m=﹣![]() ;②m=﹣2.
;②m=﹣2.
【解析】
试题分析:(1)由抛物线的顶点式可求得其顶点坐标,由伴随直线的定义可求得伴随直线的解析式,联立伴随直线和抛物线解析式可求得其交点坐标;
(2)①可先用m表示出A、B、C、D的坐标,利用勾股定理可表示出AC2、AB2和BC2,在Rt△ABC中由勾股定理可得到关于m的方程,可求得m的值;②由B、C的坐标可求得直线BC的解析式,过P作x轴的垂线交BC于点Q,则可用x表示出PQ的长,进一步表示出△PBC的面积,利用二次函数的性质可得到m的方程,可求得m的值.
试题解析:(1)∵y=(x+1)2﹣4,∴顶点坐标为(﹣1,﹣4),
由伴随直线的定义可得其伴随直线为y=(x+1)﹣4,即y=x﹣3,
联立抛物线与伴随直线的解析式可得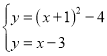 ,解得
,解得![]() 或
或![]() ,
,
∴其交点坐标为(0,﹣3)和(﹣1,﹣4),
故答案为:(﹣1,﹣4);y=x﹣3;(0,﹣3);(﹣1,﹣4);
(2)①∵抛物线解析式为y=m(x﹣1)2﹣4m,
∴其伴随直线为y=m(x﹣1)﹣4m,即y=mx﹣5m,
联立抛物线与伴随直线的解析式可得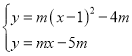 ,解得
,解得![]() 或
或![]() ,
,
∴A(1,﹣4m),B(2,﹣3m),
在y=m(x﹣1)2﹣4m中,令y=0可解得x=﹣1或x=3,
∴C(﹣1,0),D(3,0),
∴AC2=4+16m2,AB2=1+m2,BC2=9+9m2,
∵∠CAB=90°,
∴AC2+AB2=BC2,即4+16m2+1+m2=9+9m2,解得m=![]() (抛物线开口向下,舍去)或m=﹣
(抛物线开口向下,舍去)或m=﹣![]() ,
,
∴当∠CAB=90°时,m的值为﹣![]() ;
;
②设直线BC的解析式为y=kx+b,∵B(2,﹣3m),C(﹣1,0),∴![]() ,解得
,解得![]() ,
,
∴直线BC解析式为y=﹣mx﹣m,
过P作x轴的垂线交BC于点Q,如图,
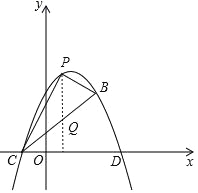
∵点P的横坐标为x,
∴P(x,m(x﹣1)2﹣4m),Q(x,﹣mx﹣m),
∵P是直线BC上方抛物线上的一个动点,
∴PQ=m(x﹣1)2﹣4m+mx+m=m(x2﹣x﹣2)=m[(x﹣![]() )2﹣
)2﹣![]() ],
],
∴S△PBC=![]() ×[(2﹣(﹣1)]PQ=
×[(2﹣(﹣1)]PQ=![]() (x﹣
(x﹣![]() )2﹣
)2﹣![]() m,
m,
∴当x=![]() 时,△PBC的面积有最大值﹣
时,△PBC的面积有最大值﹣![]() m,
m,
∴S取得最大值![]() 时,即﹣
时,即﹣![]() m=
m=![]() ,解得m=﹣2.
,解得m=﹣2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年四月份,某校在孝感市争创“全国文明城市” 活动中,组织全体学生参加了“弘扬孝感文化,争做文明学生”知识竞赛,赛后随机抽取了部分参赛学生的成绩,按得分划分成
 六个等级,并绘制成如下两幅不完整的统计图表.
六个等级,并绘制成如下两幅不完整的统计图表.

请根据图表提供的信息,解答下列问题:
(1)本次抽样调查样本容量为 ,表中:
 ,
, ;扇形统计图中,
;扇形统计图中, 等级对应的圆心角
等级对应的圆心角 等于 度;(4分=1分+1分+1分)
等于 度;(4分=1分+1分+1分)(2)该校决定从本次抽取的
 等级学生(记为甲、乙、丙、丁)中,随机选择
等级学生(记为甲、乙、丙、丁)中,随机选择 名成为学校文明宣讲志愿者,请你用列表法或画树状图的方法,求恰好抽到甲和乙的概率.
名成为学校文明宣讲志愿者,请你用列表法或画树状图的方法,求恰好抽到甲和乙的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】将多项式mn2+2mn+m因式分解的结果是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:一个正数的两个平方根分别是2a﹣2和a﹣4,则a的值是 2 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】 为满足社区居民健身的需要,市政府准备采购若干套健身器材免费提供给社区,经考察,劲松公司有
 两种型号的健身器可供选择.
两种型号的健身器可供选择.(1)劲松公司2015年每套
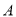 型健身器的售价为
型健身器的售价为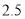 万元,经过连续两年降价,2017年每套售价为
万元,经过连续两年降价,2017年每套售价为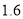 万元,求每套
万元,求每套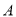 型健身器年平均下降率
型健身器年平均下降率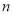 ;
;(2)2017年市政府经过招标,决定年内采购并安装劲松公司
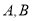 两种型号的健身器材共
两种型号的健身器材共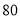 套,采购专项费总计不超过
套,采购专项费总计不超过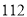 万元,采购合同规定:每套
万元,采购合同规定:每套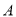 型健身器售价为
型健身器售价为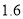 万元,每套
万元,每套 型健身器售价我
型健身器售价我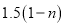 万元.
万元.①
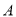 型健身器最多可购买多少套?
型健身器最多可购买多少套? ②安装完成后,若每套
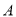 型和
型和 型健身器一年的养护费分别是购买价的
型健身器一年的养护费分别是购买价的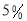 和
和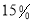 .市政府计划支出
.市政府计划支出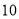 万元进行养护.问该计划支出能否满足一年的养护需要?
万元进行养护.问该计划支出能否满足一年的养护需要? -
科目: 来源: 题型:
查看答案和解析>>【题目】下列选项中表示两个全等的图形的是( )
A. 形状相同的两个图形 B. 周长相等的两个图形
C. 面积相等的两个图形 D. 能够完全重合的两个图形
-
科目: 来源: 题型:
查看答案和解析>>【题目】 已知关于
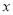 的一元二次方程
的一元二次方程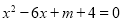 有两个实数根
有两个实数根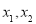 .
. (1)求
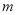 的取值范围;
的取值范围;(2)若
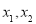 满足
满足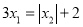 ,求
,求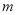 的值.
的值.
相关试题

