【题目】如图,在等边△ABC中,点D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F. 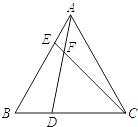
(1)求证:AD=CE;
(2)求∠DFC的度数.
参考答案:
【答案】
(1)证明:∵△ABC是等边三角形,
∴∠BAC=∠B=60°,AB=AC.
又∵AE=BD,
∴△AEC≌△BDA(SAS).
∴AD=CE
(2)解:
∵(1)△AEC≌△BDA,
∴∠ACE=∠BAD,
∴∠DFC=∠FAC+∠ACF=∠FAC+∠BAD=∠BAC=60°
【解析】根据等边三角形的性质,利用SAS证得△AEC≌△BDA,所以AD=CE,∠ACE=∠BAD,再根据三角形的外角与内角的关系得到∠DFC=∠FAC+∠ACF=∠FAC+∠BAD=∠BAC=60°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某个商贩同时卖出两件上衣,售价都是140元.按成本计算,其中一件盈利75%,另一件亏损30%,在这次交易中,该商贩( )
A.不赔不赚
B.赚10元
C.赔10元
D.赔20元 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线y=﹣x+3与x轴交于点C,与直线AD交于点A(
 ,
, ),点D的坐标为(0,1)
),点D的坐标为(0,1)(1)求直线AD的解析式;
(2)直线AD与x轴交于点B,若点E是直线AD上一动点(不与点B重合),当△BOD与△BCE相似时,求点E的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】读句画图并回答问题:
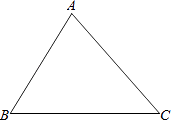
(1)过点A画AD⊥BC,垂足为D.比较AD与AB的大小:ADAB;
(2)用直尺和圆规作∠CDE,使∠CDE=∠ABC,且与AC交于点E.此时DE与AB的位置关系是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】小彬一家人在2013年8月到北京旅游了4天,这4天的日期数(如8月1日的日期数为1)之和是38,则他们一家在北京旅游最后一天的日期数是( )
A.8号
B.9号
C.10号
D.11号 -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面对话: 小红妈:“售货员,请帮我买些梨.”
售货员:“小红妈,您上次买的那种梨都卖完了,我们还没来得及进货,我建议这次您买些新进的苹果,价格比梨贵一点,不过苹果的营养价值更高.”
小红妈:“好,你们很讲信用,这次我照上次一样,也花30元钱.”
对照前后两次的电脑小票,小红妈发现:每千克苹果的价格是梨的1.5倍,苹果的重量比梨轻2.5千克.
试根据上面对话和小红妈的发现,分别求出梨和苹果的单价. -
科目: 来源: 题型:
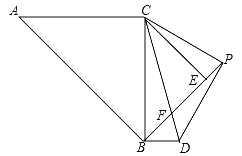
查看答案和解析>>【题目】如图,△ABC和△BEC均为等腰直角三角形,且∠ACB=∠BEC=90°,AC=
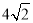 ,点P为线段BE延长线上一点,连接CP以CP为直角边向下作等腰直角△CPD,线段BE与CD相交于点F
,点P为线段BE延长线上一点,连接CP以CP为直角边向下作等腰直角△CPD,线段BE与CD相交于点F(1)求证:
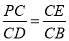 ;
;(2)连接BD,请你判断AC与BD有什么位置关系?并说明理由;
(3)设PE=x,△PBD的面积为S,求S与x之间的函数关系式.
相关试题

