【题目】A、B两地相距70千米,甲从A地出发,每小时行15千米,乙从B地出发,每小时行20千米.
(1)若两人同时出发,相向而行,则经过几小时两人相遇?
(2)若甲在前,乙在后,两人同时同向而行,则几小时后乙追上甲?
(3)若两人同时出发,相向而行,则几小时后两人相距10千米?
参考答案:
【答案】(1)经过2小时两人相遇;(2)经过14小时,乙追上甲;(3)![]() 小时或
小时或![]() 小时后两人相距10千米.
小时后两人相距10千米.
【解析】
(1)设经过x小时两人相遇,根据甲走的路程+乙走的路程= A、B两地相距的路程70千米列出方程,解方程即可求解;(2)设经过a小时,乙追上甲,根据乙走的路程=甲走的路程+ A、B两地相距的路程列出方程,解方程即可求解;(2)设b小时后两人相距10千米,根据相遇前甲乙相距10千米和相遇后甲乙相距10千米列出方程,解方程即可求解.
解:(1)设经过x小时两人相遇,
15x+20x=70,
解得,x=2,
答:经过2小时两人相遇;
(2)设经过a小时,乙超过甲10千米,
20a=15a+70,
解得,a=14,
答:经过14小时,乙超过甲10千米;
(3)设b小时后两人相距10千米,
|15b+20b﹣70|=10,
解得,b1=![]() ,b2=
,b2=![]() ,
,
答:![]() 小时或
小时或![]() 小时后两人相距10千米.
小时后两人相距10千米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个正方体的平面展开图,标注了A字母的是正方体的正面,如果正方体的左面与右面标注的式子相等.

(1)求x的值.
(2)求正方体的上面和底面的数字和.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在坐标系中作出函数y=2x+6 的图象,利用图象解答下列问题:
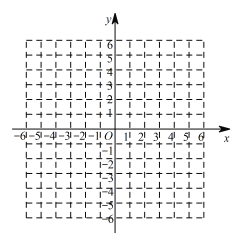
(1)求方程2x+6=0 的解;
(2)求不等式2x+6>4 的解集;
(3)若-2≤y≤2 ,求 x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,对于任意三点A,B,C,给出如下定义:
如果矩形的任何一条边均与某条坐标轴平行,且A,B,C三点都在矩形的内部或边界上,则称该矩形为点A,B,C的覆盖矩形.点A,B,C的所有覆盖矩形中,面积最小的矩形称为点A,B,C的最优覆盖矩形.例如,下图中的矩形A1B1C1D1 , A2B2C2D2 , AB3C3D3都是点A,B,C的覆盖矩形,其中矩形AB3C3D3是点A,B,C的最优覆盖矩形.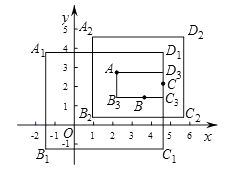
(1)已知A(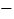 2,3),B(5,0),C(
2,3),B(5,0),C(  ,
, 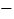 2).
2).
①当 时,点A,B,C的最优覆盖矩形的面积为;
时,点A,B,C的最优覆盖矩形的面积为;
②若点A,B,C的最优覆盖矩形的面积为40,则t的值为;
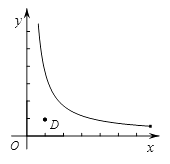
(2)已知点D(1,1),点E(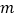 ,
, 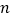 ),其中点E是函数
),其中点E是函数 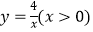 的图像上一点,⊙P是点O,D,E的一个面积最小的最优覆盖矩形的外接圆,求出⊙P的半径r的取值范围.
的图像上一点,⊙P是点O,D,E的一个面积最小的最优覆盖矩形的外接圆,求出⊙P的半径r的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】今年9月,莉莉进入八中初一,在准备开学用品时,她决定购买若干个某款笔记本,甲、乙两家文具店都有足够数量的该款笔记本,这两家文具店该款笔记本标价都是20元/个.甲文具店的销售方案是:购买该笔记本的数量不超过5个时,原价销售;购买该笔记本超过5个时,从第6个开始按标价的八折出售:乙文具店的销售方案是:不管购买多少个该款笔记本,一律按标价的九折出售.
(1)若设莉莉要购买x(x>5)个该款笔记本,请用含x的代数式分别表示莉莉到甲文具店和乙文具店购买全部该款笔记本所需的费用;
(2)在(1)的条件下,莉莉购买多少个笔记本时,到乙文具店购买全部笔记本所需的费用与到甲文具店购买全部笔记本所需的费用相同?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,已知直线l1:y=mx(m≠0) 与直线l2:y=ax+b(a≠0) 相交于点 A(1,2),直线l2与 x轴交于点B(3,0).
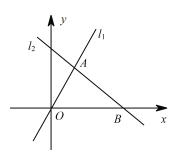
(1)分别求直线l1 和l2的表达式;
(2)过动点P(0,n)且平行于x轴的直线与l1 ,l2的交点分别为C ,D,当点 C 位于点 D 左方时,写出 n的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上有三个点
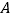 、
、 、
、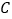 ,如图所示.
,如图所示.
(1)将点
 向左平移4个单位,此时该点表示的数是________;
向左平移4个单位,此时该点表示的数是________; (2)将点
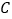 向左平移3个单位得到数
向左平移3个单位得到数 ,再向右平移2个单位得到数
,再向右平移2个单位得到数 ,则
,则 ,
, 分别是多少?
分别是多少? (3)怎样移动
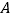 、
、 、
、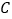 中的两点,使三个点表示的数相同?你有几种方法?
中的两点,使三个点表示的数相同?你有几种方法?
相关试题

