【题目】求出抛物线的开口方向、对称轴、顶点坐标.
(1)y=x2+2x﹣3(配方法);
(2)y= ![]() x2﹣x+3(公式法).
x2﹣x+3(公式法).
参考答案:
【答案】
(1)解:y=x2+2x﹣3=x2+2x+1﹣4
=(x+1)2﹣4,
所以抛物线的开口向上,对称轴为直线x=﹣1,顶点坐标为(﹣1,﹣4)
(2)解:﹣ ![]() =﹣
=﹣ ![]() =1,
=1, ![]() =
= 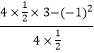 =
= ![]() ,
,
所以抛物线的开口向上,对称轴为直线x=1,顶点坐标为(1, ![]() ).
).
【解析】(1)先依据a的正负判断出抛物线的开口方向,然后依据进行配方,将抛物线的解析式变形为y=a(x-h)2+k的形式,然后可得到抛物线的对称轴和顶点坐标;
(2)先依据a的正负判断出抛物线的开口方向,然后抛物线的顶点坐标公式和对称轴公式求解即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△DAC和△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N,且A、C、B在同一直线上,有如下结论:①△ACE≌△DCB;②CM=CN;③AC=DN;④PC平分∠APB;⑤∠APD=60°,其中正确结论有( )

A. 5个 B. 4个 C. 3个 D. 2个
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算.
(1)|﹣3|﹣(
 )﹣2+(
)﹣2+(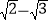 )0
)0(2)(﹣3m2n)2(﹣2m2)÷6mn2
(3)2x(x﹣
 y)﹣(x+2y)(x﹣y)
y)﹣(x+2y)(x﹣y)(4)[(x﹣2y)2﹣x(x﹣4y)﹣8xy]÷4y
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列算式:
①1×3-22=3-4=-1;
②2×4-32=8-9=-1;
③3×5-42=15-16=-1;
…
(1)请按照以上规律写出第10个等式。
(2)请按照以上规律写出第n个等式。
(3)(2)中的式子一定成立吗?若不一定成立,请举出反例;若一定成立,请说出理由。
-
科目: 来源: 题型:
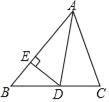
查看答案和解析>>【题目】已知△ABC中,∠B=50°,∠C=70°,AD是△ABC的角平分线,DE⊥AB于E点.
(1)求∠EDA的度数;
(2)AB=10,AC=8,DE=3,求S△ABC.
-
科目: 来源: 题型:
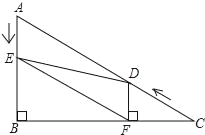
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,AC=10,∠C=30°点D从点C出发沿CA方向以每秒2个单位长度的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长度的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0),过点D作DF⊥BC于点F,连接DE、EF.
(1)DF= ;(用含t的代数式表示)
(2)求证:△AED≌△FDE;
(3)当t为何值时,△DEF是等边三角形?说明理由;
(4)当t为何值时,△DEF为直角三角形?(请直接写出t的值.)
-
科目: 来源: 题型:
查看答案和解析>>【题目】一家商店进行门店升级需要装修,装修期间暂停营业,若请甲乙两个装修组同时施工,8天可以完成,需付费用共3520元;若先请甲组单独做6天,再请乙组单独做12天可以完成,需付费用3480元,问:
(1)甲、乙两组工作一天,商店各应付多少钱?
(2)已知甲组单独完成需12天,乙组单独完成需24天,单独请哪个组,商店所需费用最少?
(3)装修完毕第二天即可正常营业,且每天仍可盈利200元(即装修前后每天盈利不变),你认为商店应如何安排施工更有利?说说你的理由.(可用(1)(2)问的条件及结论)
相关试题

