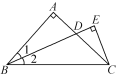
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,∠1=∠2,CE⊥BD交BD的延长线于点E.求证:BD=2CE.
参考答案:
【答案】证明见解析.
【解析】
延长CE、BA交于F,根据角边角定理,证明△BEF≌△BEC,进而得到CF=2CE的关系.再证明∠ACF=∠1,根据角边角定理证明△ACF≌△ABD,得到BD=CF,至此问题得解.
证明:分别延长BA,CE交于点F.
∵BE⊥CE,
∴∠BEF=∠BEC=90°.
又∵∠1=∠2,BE=BE,
∴△BEF≌△BEC(ASA),
∴CE=FE=![]() CF.
CF.
∵∠1+∠F=90°,∠ACF+∠F=90°,
∴∠1=∠ACF.又∵AB=AC,∠BAD=∠CAF=90°,
∴△ABD≌△ACF(ASA),
∴BD=CF,
∴BD=2CE
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1的正方形网格中,△ABC的顶点均在格点上,点A、B的坐标分别是A(5,3)、B(5,1).

(1)在图中标出△ABC外心D的位置,并直接写出它的坐标;
(2)判断△ABC的外接圆D与x轴、y轴的位置关系,并说明理由. -
科目: 来源: 题型:
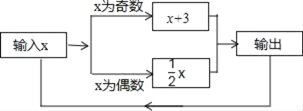
查看答案和解析>>【题目】金湖中学社团活动开展地丰富多彩.七年级数学社团课上同学们在探究一数值转换器,原理如图所示.开始输入x值为5,可发现第一次输出的结果是8,第2次输出结果是4,依次下去…,第2018次输出的结果是__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用黑白两种颜色的正六边形地砖按如下所示的规律拼成若干图案:

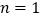
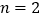
⑴ 当黑砖n=1时,白砖有_______块,当黑砖n=2时,白砖有________块,
当黑砖n=3时,白砖有_______块.
⑵ 第n个图案中,白色地砖共 块.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(背景知识)
数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合.研究数轴我们发现了许多重要的规律:若数轴上点
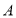 、点
、点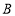 表示的数分别为
表示的数分别为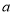 、
、 ,则
,则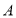 、
、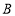 两点之间的距离
两点之间的距离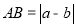 ,线段
,线段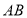 的中点表示的数为
的中点表示的数为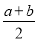 .
.(问题情境)
如图,数轴上点
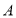 表示的数为
表示的数为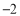 ,点
,点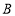 表示的数为8,点
表示的数为8,点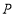 从点
从点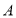 出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点
出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点 从点
从点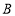 出发,以每秒2个单位长度的速度向左匀速运动,设运动时间为
出发,以每秒2个单位长度的速度向左匀速运动,设运动时间为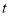 秒(
秒( ).
).(综合运用)
(1)填空:
①
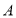 、
、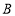 两点之间的距离
两点之间的距离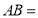 ________,线段
________,线段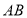 的中点表示的数为__________.
的中点表示的数为__________.②用含
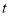 的代数式表示:
的代数式表示: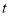 秒后,点
秒后,点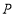 表示的数为____________;点
表示的数为____________;点 表示的数为___________.
表示的数为___________.③当
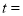 _________时,
_________时,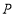 、
、 两点相遇,相遇点所表示的数为__________.
两点相遇,相遇点所表示的数为__________.(2)当
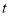 为何值时,
为何值时,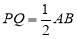 .
.(3)若点
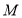 为
为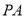 的中点,点
的中点,点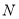 为
为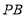 的中点,点
的中点,点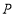 在运动过程中,线段
在运动过程中,线段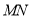 的长度是否发生变化?若变化,请说明理由;若不变,请求出线段
的长度是否发生变化?若变化,请说明理由;若不变,请求出线段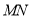 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场将每件进价为80元的某种商品原来按每件100元出售,一天可售出100件.后来经过市场调查,发现这种商品单价每降低1元,其销量可增加10件.
(1)求商场经营该商品原来一天可获利润多少元?
(2)设后来该商品每件降价x元,商场一天可获利润y元.
①若商场经营该商品一天要获利润2160元,则每件商品应降价多少元?
②求出y与x之间的函数关系式,并直接写出当x取何值时,商场获利润不少于2160元. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,⊙C的半径为r(r>1),P是圆内与圆心C不重合的点,⊙C的“完美点”的定义如下:若直线CP与⊙C交于点A,B,满足|PA﹣PB|=2,则称点P为⊙C的“完美点”,如图为⊙C及其“完美点”P的示意图.
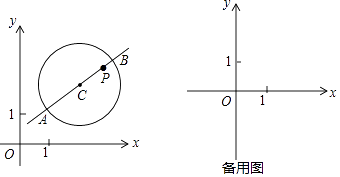
(1)当⊙O的半径为2时,
①点M( ,0)⊙O的“完美点”,点N(0,1)⊙O的“完美点”,点T(﹣
,0)⊙O的“完美点”,点N(0,1)⊙O的“完美点”,点T(﹣ 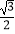 ,﹣
,﹣  )⊙O的“完美点”(填“是”或者“不是”);
)⊙O的“完美点”(填“是”或者“不是”);
②若⊙O的“完美点”P在直线y=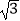 x上,求PO的长及点P的坐标;
x上,求PO的长及点P的坐标;
(2)⊙C的圆心在直线y=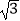 x+1上,半径为2,若y轴上存在⊙C的“完美点”,求圆心C的纵坐标t的取值范围.
x+1上,半径为2,若y轴上存在⊙C的“完美点”,求圆心C的纵坐标t的取值范围.
相关试题

