【题目】如图,在△ABC中,AB=AC,∠BAC=90°,BD平分∠ABC,交AC于点D,AF⊥BD,垂足为点E,交BC于点F.求证:AD=CF.

参考答案:
【答案】见解析
【解析】
作辅助线,证明∠BAG=∠C=45°,再利用同角的余角相等得∠ABG=∠CAF,证明△ABG≌△CAF(ASA),得到AG=CF,最后证明△GAE≌△DAE(ASA),等量代换即可解题.
证明:过点A作∠BAC的平分线AG,交BD于点G,

∵AB=AC,
∴∠ABC=∠C.
∵∠BAC=90°,
∴∠ABC=∠C=45°.
∵AG平分∠BAC,
∴∠BAG=∠CAG=![]() ∠ABC=45°,
∠ABC=45°,
∴∠BAG=∠C.
∵AE⊥BD,
∴∠ABG+∠BAE=90°.
∵∠CAF+∠BAE=90°,
∴∠ABG=∠CAF.
在△ABG和△CAF中, ,
,
∴△ABG≌△CAF(ASA),
∴AG=CF.

∵BD平分∠ABC,
∴∠ABG=∠CAF,
∴∠CAF=22.5°.
∵∠CAG=45°,
∴∠GAE=∠CAG-∠CAF=45-22.5°=22.5°,
∴∠GAE=∠CAF.
∵AE⊥BD,
∴∠AEG=∠AED=90°.
在△GAE和△DAE中, ,
,
∴△GAE≌△DAE(ASA),
∴AG=AD.
∵AG=CF,
∴AD=CF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国著名数学家华罗庚曾经说过,“数形结合百般好,隔裂分家万事非。”数形结合的思想方法在数学中应用极为广泛.
观察下列按照一定规律堆砌的钢管的横截面图:
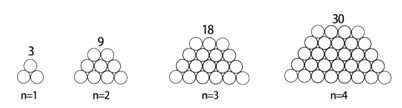
用含n的式子表示第n个图的钢管总数.
(分析思路)
图形规律中暗含数字规律,我们可以采用分步的方法,从图形排列中找规律;把图形看成几个部分的组合,并保持结构,找到每一部分对应的数字规律,进而找到整个图形对应的数字规律。
如:要解决上面问题,我们不妨先从特例入手:(统一用S表示钢管总数)
(解决问题)
(1)如图,如果把每个图形按照它的行来分割观察,你发现了这些钢管的堆砌规律了吗?像n=1、n=2的情形那样,在所给横线上,请用数学算式表达你发现的规律.

S=1+2 S=2+3+4 _____________ ______________
(2)其实,对同一个图形,我们的分析眼光可以是不同的。请你像(1)那样保持结构的、对每一个所给图形添加分割线,提供与(1)不同的分割方式;并在所给横线上,请用数学算式表达你发现的规律:

_______ ____________ _______________ _______________
(3)用含n的式子列式,并计算第n个图的钢管总数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴正半轴相交于A、B两点,与y轴相交于点C,对称轴为直线x=2,且OA=OC,则下列结论: ①abc>0;②9a+3b+c<0;③c>﹣1;
④关于x的方程ax2+bx+c=0(a≠0)有一个根为﹣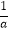
其中正确的结论个数有(填序号)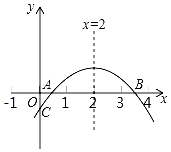
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点O到△ABC的两边AB,AC所在直线的距离相等,且OB=OC.
(1)如图①,若点O在边BC上,求证:AB=AC;
(2)如图②,若点O在△ABC的内部,求证:AB=AC;
(3)若点O在△ABC的外部,AB=AC成立吗?请画图表示.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校在践行“社会主义核心价值观”演讲比赛中,对名列前20名的选手的综合分数m进行分组统计,结果如表所示:
组号
分组
频数
一
6≤m<7
2
二
7≤m<8
7
三
8≤m<9
a
四
9≤m≤10
2
(1)求a的值;
(2)若用扇形图来描述,求分数在8≤m<9内所对应的扇形图的圆心角大小;
(3)将在第一组内的两名选手记为:A1、A2 , 在第四组内的两名选手记为:B1、B2 , 从第一组和第四组中随机选取2名选手进行调研座谈,求第一组至少有1名选手被选中的概率(用树状图或列表法列出所有可能结果).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,线段AB=CD,AB与CD相交于点O,且∠AOC=60°,CE是由AB平移所得,AC与BD不平行,则AC+BD与AB的大小关系是:AC+BD_____AB.(填“>”“<”或“=”)

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知m,n是小于5的正整数,且
 =a﹣b,求m,n的值.
=a﹣b,求m,n的值.
相关试题

